为适应人类不断增长的欲望和野心,结构工程师的胆量渐长,房子越修越高,跨度越修越大,同时材料也越用越省,于是结构稳定性的问题就越来越突出。
规范中结构稳定性三个层面的要求
现行规范从三个层次对结构的稳定性做出了要求:
(1)整体层面。高砼规和高钢规分别给出了刚重比的要求;广东高规提出如果采用特征值屈曲判定结构整体稳定性时,第一屈曲因子(此系数非真实安全系数)不得小于10;空间网格规程要求当考虑几何非线性不考虑材料非线性时稳定性安全系数(此系数非真实安全系数)不得小于4.2,当同时考虑几何非线性及材料非线性时稳定安全系数(此系数为真实安全系数)不得小于2。
(2)构件层面。规范主要通过引入柱计算长度系数,构造上控制长细比,并验算稳定承载力或稳定应力。部分柱无法按规范确定计算长度系数所以需要通过特征值屈曲分析获得,也即本文重点讨论的内容。
(3)板件层面。就是所谓的局部屈曲,规范通过宽厚比或高厚比等构造保证。
整体、构件及板件三个层面的稳定性问题,只要能灵活使用均可通过屈曲分析(特征值屈曲分析或非线性屈曲分析)进行评价,所以不可小看屈曲分析。
对柱计算长度系数的认识及软件的处理
(1)柱的计算长度系数不影响整体结构或构件的刚度,所以也不影响构件的轴力、弯矩及剪力等内力标准值。柱的计算长度系数仅影响构件设计阶段长细比的验算,以及稳定承载力或稳定应力的验算。
(2)对于跃层柱国产主流设计软件已主动进行了处理,YJK是合并层高修正柱几何长度,PKPM是直接修正柱计算长度系数,需要核实无误后使用。
(3)对于钢管砼柱国产主流软件一般按纯钢结构计算不正确,需要进行修正。简单的可以直接参照混凝土柱。
(4)对于支撑网架等柱顶为铰接的混凝土柱国产主流设计软件一般按砼规中框架结构取值不正确,应按排架结构取值进行修改。
欧拉公式

瑞士伟大的数学家、科学家欧拉生平提出了N多公式,今天我们只用其中之一来求解受压构件的计算长度系数:
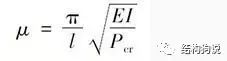
式中Pcr即为弹性临界承载力,注意这个承载力并不是真实的极限承载力,原因就在于弹性的假定。
对于理想的约束情况,计算长度系数如下:两端铰接1.0,两端固接0.5;一端固接一端铰接0.7;悬臂2.0。但由于构件处于整体结构这个复杂的大环境,它的计算长度系数就没有那么单纯了。简单的情况可以根据规范取值,复杂情况就得根据特征值屈曲分析获取了。
对特征值屈曲分析的认识
特征值屈曲分析(或线性屈曲分析)和无阻尼自由振动求解结构自振周期类似,各阶模态表示发生该种屈曲的可能性,越靠前表明发生该屈曲变形的可能性越大。各阶模态中有结构整体的屈曲,也有构件层面的屈曲,要进行识别。如果要观察板件层面的局部屈曲需要实体或壳单元来详细模拟梁柱支撑等杆件才能被识别。求解得出的特征值乘以柱初始的轴力即为弹性极限承载力Pcr。
整体屈曲VS构件屈曲
一般情况下,进行特征值屈曲分析前几阶模态为整体屈曲。广东高规要求的屈曲因子大于10一般指的是第一阶模态。不知道小伙伴们如何区别整体屈曲和构件屈曲,小编认为当梁柱为刚接时,若柱高范围内出现了至少两个反弯点即可判断为柱屈曲(构件屈曲)。可用塑料尺做个简单的试验,中图为标准的两端固接出现了三个反弯点。
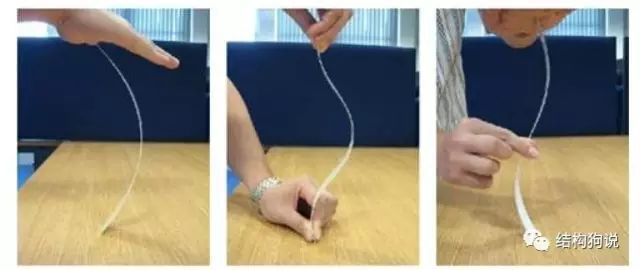
左(两端铰接)中(两端固接)右(上端固接下端铰接中部约束)(图片来源网络)
柱计算长度系数求解过程
进行一个简单的钢框架特征值屈曲分析,跃层柱初始轴力500KN,无梁支撑一侧柱高6m(层高3m)。
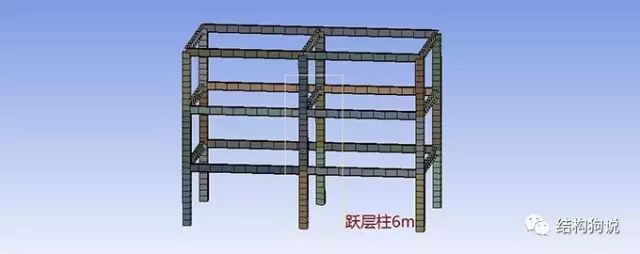
由于此模型体量较小,且突出了跃层柱的不利影响,第一模态便出现了跃层柱屈曲,虽然不是很明显但第一模态跃层柱确实出现了两个反弯点。该模态屈曲特征值为25,求得跃层柱弹性极限承载力为12500KN,但实际上不可能这么大,原因前面已经解释过了。由此求得跃层柱计算长度系数为1.34(YJK根据钢规确定的计算长度系数为1.52)。
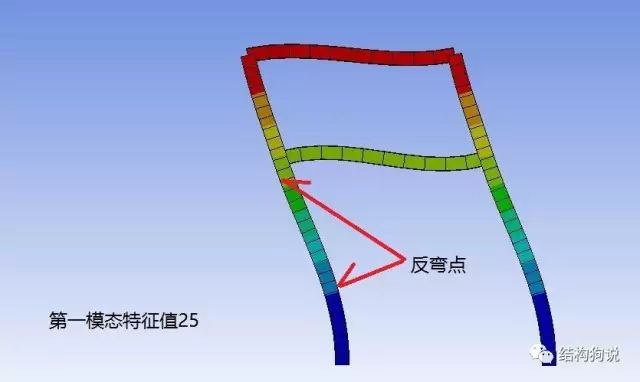
下面再看一个跃层柱屈曲更明显的模态:
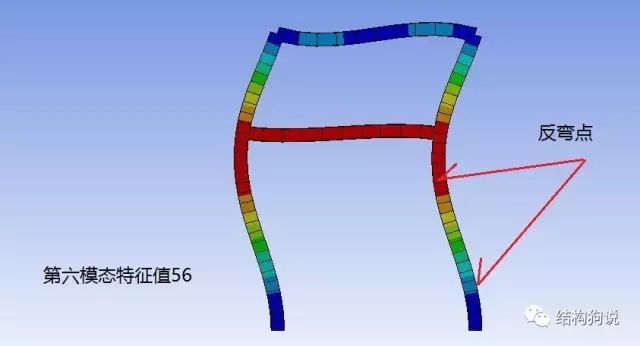
钢管砼柱计算长度系数实例
《建筑结构》2015年11月下《曲靖金都佳园1栋塔楼结构分析》截选。(结构概括:建筑高度218m,结构形式框架-核心筒,外框柱采用钢管砼柱,设计类软件按纯钢结构计算钢管砼柱计算长度系数不正确,故需要自行计算)




受压构件真实极限承载力
柱或受压构件真实的竖向极限承载力需要通过非线性屈曲分析获取。非线性屈曲分析只是听起来高大上,其原理比Pushover静力弹塑性分析更简单,将在今后的文章中进行讨论。
END