ganggouren
来源：公众号“胡正宇结构视点” 作者：胡正宇
作者：胡正宇，英国皇家结构工程师学会(IStructE)资深会士(Fellow)，加拿大安省分会主席(Chairman of IStructE Ontario Division)，现持有英国皇家注册结构工程师、加拿大ON/AB/BC省注册工程师 Professional Engineer (P.Eng.)、BC省特别指定结构工程师 Designated Structural Engineer (Struct.Eng.) 以及中国一级注册结构工程师等诸多国家和地区的顶级结构工程设计从业资质。胡正宇先生目前还是美国土木工程师协会正式会员(M.ASCE)，并兼任英国皇家结构工程师学会皇家注册结构工程师考试阅卷考官（Marking Examiner of IStructE Chartered Membership Exam）。胡先生拥有超过二十年国际工程设计经验，精通从超高层到大跨度等各种结构类型的设计及项目管理。现为加拿大国家转自：规范(CSA-S16)技术委员会委员，也是中国现行构筑物抗震规范GB50191-2012主要起草人之一。
编者按：从本周开始，除了综述性的文章外，我将会在每周的公众号文章中择机介绍一些结构设计中的重要的技术点，同时将结合现行中国，美国及加拿大的相关结构规范对此问题的处理方法进行逐点对比介绍，并给出作者建议或点评，以供各位同行朋友参考。今天我们首先来谈一谈工字形截面钢悬臂梁的整体稳定承载力以及有效计算长度系数问题。这个话题其实对做结构设计的同行并不陌生，我也曾听到过一些结构工程师在指导年轻刚入行的工程师工作时提醒道：“不要把悬臂梁的计算长度系数搞错，应该是2不是1！”，可真的是这样的吗？今天我们就来仔细聊一聊这个话题。需要特别说明的是：以下文中所涉及的所有相关公式及图片均收集整理自文末索引的规范或论文，且本文并非学术性论文，仅为一般技术笔记性文章，所以尽管作者已对相关资料作了仔细检查及推敲验证，但仍不免会存在错漏之处，敬请各位见谅。
我们在学结构力学时，对于一端固接的悬臂杆件的理论杆件计算长度系数我们一般理想化地取2，所以有些工程师就想当然的把这一原则应用在钢结构悬臂梁的设计中。有些有经验的工程师可能会意识到这样做是有一定问题的，因为学过钢结构稳定的朋友都知道，受弯作用下的悬臂梁的弹性弯扭屈曲承载力（Lateral Torsional Buckling Resistance）是与梁的嵌固端的约束情况，梁身的侧向支撑条件，荷载分布形式以及荷载作用位置密切相关，不同的约束条件及荷载条件所对应的弹性弯扭屈曲承载力是不一样的。可是如何在结构设计中定量地考察这些约束和荷载条件对悬臂梁的承载力影响呢？很多人第一反应是：查规范！好吧，那么我们就来看一看规范中就这一问题是如何规定的。
中国钢规 (GB50017-2017)
首先来看看中国的现行转自：规范GB50017-2017对这一问题是怎么处理的。在GB50017-2017对于受弯构件整体稳定是这么说的：规范条文 6.2.1：当铺板密铺在梁的受压翼缘上并与其牢固相连，能阻止梁受压翼缘的侧向位移时，可不计算梁的整体稳定性；规范条文 6.2.2：除本标准第 6.2.1 条所指情况外，在最大刚度主平面内受弯的构件，其整体稳定性应按下式计算：
对所有受弯构件均采用上式验算。因此这里的关键点就是如何确定这个梁的整体稳定系数φb，根据规范附录C确定。那么我们来看看附录C是如何规定的。翻到附录C，等截面焊接工字形和轧制H 型钢（图 C.0.1）简支梁的整体稳定系数φb应按下列公式计算。公式貌似很复杂，其实你只要记住这个φb是由一个同构件长细比及截面形式及尺寸相关的一组数（如下式虚线框中所示）与一个神秘的βb系数（下式中绿色高亮背景文字）的乘积即可。这个βb系数又是另一个关于与梁截面尺寸及长度相关的参数线性拟合而得。因此整个φb公式的确定即是对多组构件截面尺寸，形式及长度的相关试验结果的多重数学拟合所得。所以公式的本身不具有任何力学意义。（这种操作是中外许多规范公式中经常采用的数学游戏，区别就是有些公式中的项的力学物理意义要多些，有些少些，仅此而已。后面我在介绍美加规范公式时还会谈到。）所以形式上很复杂，但逻辑上很好理解。
现在回到悬臂梁，关于悬臂梁的整体稳定系数如下所示。
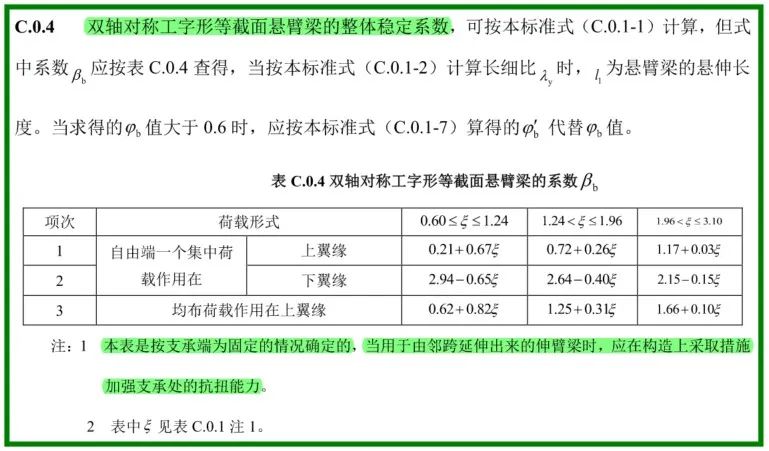问题来了，细心的读者可能会立刻注意到表下方的小注1：“本表是按支承端为固定的情况确定的，当用于由邻跨延伸出来的伸臂梁时，应在构造上采取措施加强支承处的抗扭能力。” 试问有多少设计钢悬臂梁是按支承端为理想固端而不是由邻跨延伸出来的伸臂梁呢？显然由邻跨延伸出来的悬臂梁应该是很常见的，但对此应如何设计计算呢？规范没有给出规定，仅要求构造采取措施加强一笔带过。那么怎么个构造加强才“够”加强支承处的抗扭能力？如何定量地判定？如果不够怎么办？按照中国钢规，此问题似乎不能得到一个圆满的解答了。
美国钢规 (AISC 360-16)
那么我们再来看看现行美国钢规（AISC 360-16）是怎么处理这个问题的。无侧向支撑钢梁的整体稳定计算时在现行美规第F2章给出的，其基本思路是对钢梁的侧向无支撑长度给出两个临界长度Lp 和Lr， 当钢梁实际的侧向无支撑长度小于Lp时，不会发生弹性弯扭屈曲（Elastic Lateral-Torsional Buckling）而只会发生梁的屈服破坏；而当钢梁实际的侧向无支撑长度大于Lr 时只会发生弹性弯扭屈曲（Elastic Lateral-Torsional Buckling）；当钢梁实际的侧向无支撑长度介于Lp和Lr两者之间时，钢梁的整体稳定处于过渡状态，即会发生非弹性弯扭屈曲（Inelastic Lateral-Torsional Buckling），规范给出相应的公式对应这三种不同的状态，如下所示：
需要注意的是，以上公式中F2-3和F2-4 是对前一版规范公式（如下所示）的改写，目的是使其在形式上与单轴对称截面构件整体稳定计算公式保持一致。其结果与以下前版规范中的公式完全一致。
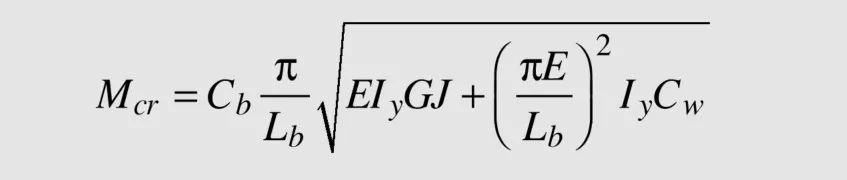
如我之前所述，设计公式的数学变换游戏是各国规范编制专家们乐此不彼的一个游戏。同样的道理，对于以上的公式，你只要记住这Mcr是由一个参数Cb与一组和梁截面形状以及侧向无支撑长度相关的数所得的乘积即可，类似中国规范中的βb*Wx。这个Cb是一个与梁沿长度方向侧向由外力作用而产生的弯矩分布形态相关的系数。与中国规范类似，美规对悬臂梁也仅仅以一句“对悬臂梁，当其支座翘曲扭转被约束时，取Cb=1.0”一笔带过。在规范正文中并无过多说明。似乎关于悬臂梁的有效计算长度及弯扭屈曲承载力也不能从美规中得到直接的解答。那么接下来我们来看看加拿大规范对这一问题是如何规定的。
加拿大规范(CSA S16-19)
现行加拿大规范2019版在第13章第13.6.1条对无侧向支撑的双轴对称截面的整体稳定承载力规定如下：
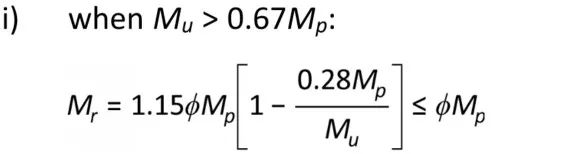
其中Mu为梁在一定的侧向无支撑长度下弹性临界弯扭屈曲弯矩，定义如下。其公式除了那个与梁沿长度方向侧向由外力作用而产生的弯矩相关的系数ω2外(美标为Cb，但二者意义完全一致，计算公式略有差异)，其余同美标完全一致，非常好理解。
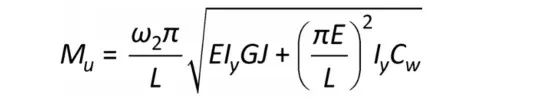
同美规的思路类似，加拿大规范将梁在不同侧向支撑条件下所得的弯扭屈曲承载力（弯矩）给出了一个临界值：0.67倍的梁截面塑性抵抗弯矩Mp。当梁的弹性临界弯扭屈曲弯矩Mu值大于0.67倍的Mp，则表明梁会发生非弹性弯扭屈曲，其承载力（弯矩）即按上i)式计算，且不大于塑性截面承载力；反之当梁在一定的侧向无支撑长度时其弹性临界弯扭屈曲弯矩Mu值不大于0.67Mp时，则表明梁会发生弹性弯扭屈曲，其承载力（弯矩）即按上ii)式计算，即仅乘以一个抗力分项系数ϕ=0.9即可。
由上公式可见，加拿大规范对于侧向无支撑梁的弯扭屈曲弯矩承载力计算与美标相比，原理基本一致，但计算更为简单（仅区分为两个计算区间，美标为三个）。那么现在我们来看看关于悬臂梁加拿大规范是如何规定的：规范13.6.1.d) 正文条文如下：
“For cantilever beams, a rational method of analysis taking into account the lateral and torsional restraint conditions at the supports and tip of the cantilever, as well as the loading conditions and the flexibility of the backspan, shall be used. For the case of fully fixed end I-shapes, Mr may be determined by the provisions of Item h).”
即“对于悬臂梁，应使用一种合理的分析方法，其中应考虑到悬臂的支座和悬臂端处的横向和扭转约束条件，荷载条件，以及和悬臂支座连续的后跨（Backspan）的刚度”。对于支座端完全固接的H形截面悬臂梁，应按13.6.1.h) 条计算其弯扭屈曲承载力Mr。“
啊哈，似乎有解决我们问题的线索，继续往下看13.6.1.h) 条：
从13.6.1.h) 条（如上所列）可见，加拿大规范给出了在支座端完全固接（限制工字形梁的扭转和翘曲）的前提下，根据荷载作用的不同位置，以及悬臂梁受拉翼缘有无支撑的情况，分别给出了不同截面类别（Class1~4）的抗弯稳定承载力。那么如何解决支座约束的影响呢？比如悬臂是由邻跨延伸出来的情况？规范13.6.1.d)中所说的“合理的分析方法“在哪里呢？终于，我们在这一条的条文说明中找到了线索。
由Ronald D. Ziemian主编的《Guide to Stability Design Criteria for Metal Structures》一书第5.2.9章节可知，Essa和Kennedy于1994提出了集中荷载作用在悬臂端的由邻跨延伸出来的悬臂梁的弯扭屈曲承载力。这里假定悬臂端的支座处（即悬臂端和后跨交汇的支点处）梁的上下翼缘同时受到侧向约束，同时假定后跨(Backspan)梁段无侧向约束。当后跨(Backspan)梁段控制整体悬臂前后跨整体稳定承载力时，他们建议悬臂梁和后跨(Backspan)的整体弯曲承载力可近似的取为在支座处翘曲受到约束时的后跨弯扭屈曲承载力Mb=Mocr，通过下式计算所得：
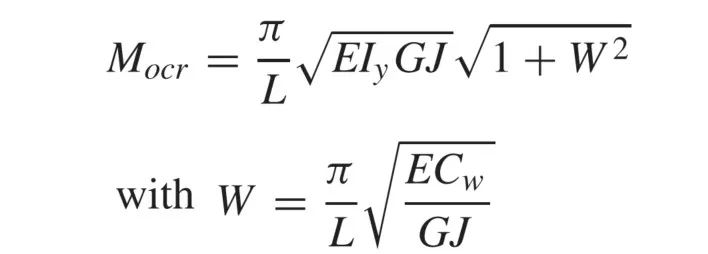
当悬臂梁段控制整体悬臂前后跨整体稳定承载力时，悬臂梁的整体稳定承载力可以写成如下形式，其中Mc为假定梁在支座处无翘曲时的悬臂段的临界稳定承载力（弯矩）：
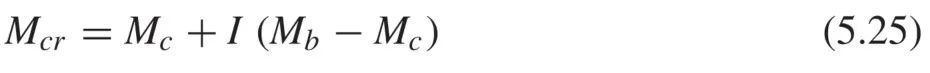
当荷载作用于梁上翼缘时，Mc如下式所示：
当荷载作用于梁的剪切中心时，Mc如下式所示：
相应地，系数I 定义如下：当梁无侧向支撑时：
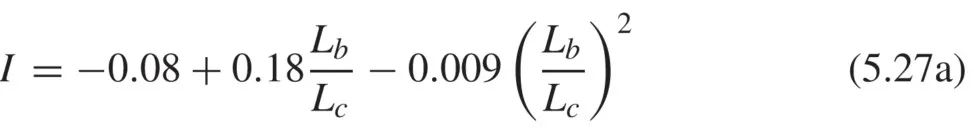
当梁端上翼缘处有侧向支撑时：
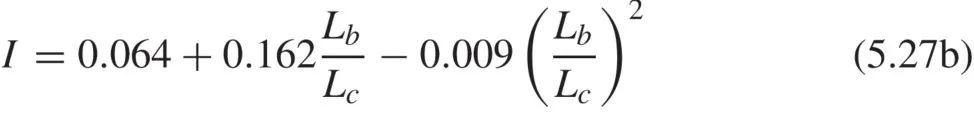
上两式中Lc为悬臂段的长度，Lb为后跨段（backspan）的长度。
至此，我们解决了由后跨延伸出来的悬臂，当假定悬臂支座处梁上下翼缘均受到侧向约束时的梁的稳定承载力。现在只剩下最后一个问题了，即当悬臂支座处梁上下翼缘无侧向约束或在不同的侧向约束条件时悬臂梁的稳定承载力该如何确定？根据加拿大规范条文说明的指引，我们在由CISC (Canadian Institution of Steel Costruction) 出版的《Roof Framing with Cantilever (Gerber) Girders & Open Web Steel Joists》一文中找到了答案。
根据Nethercot等的研究成果，可在加拿大规范中梁的临界弯扭屈曲公式中，引入一个考虑与悬臂支座处梁上下翼缘无侧向约束或在不同的侧向约束条件时所对应的计算长度系数K，将其与悬臂梁无支撑长度L相乘即可，如下式所示。（此法亦适用于美标规范，将ω2替换为Cb即可）
具体k取值如下：
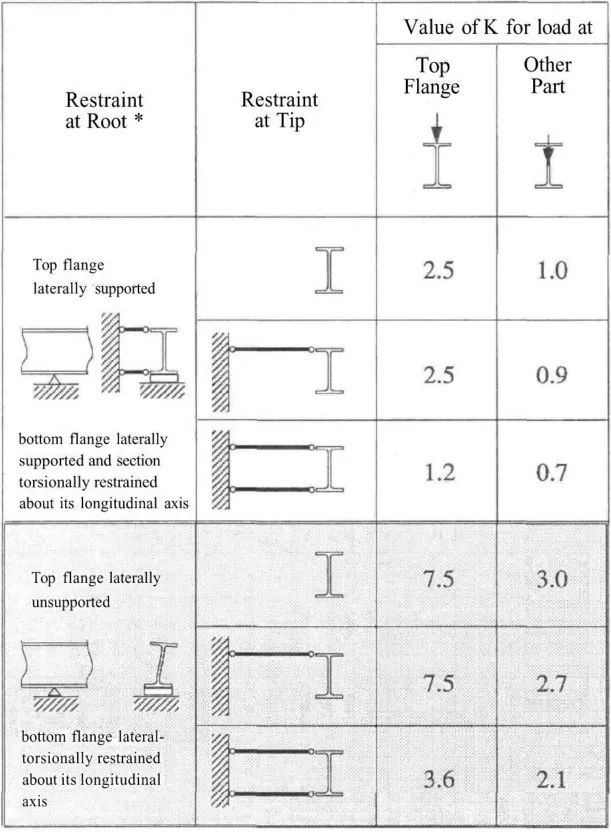
-上图中*表示支座处沿梁截面弱轴的转动自由度不受约束。
-上表中的支座定义如下所示：
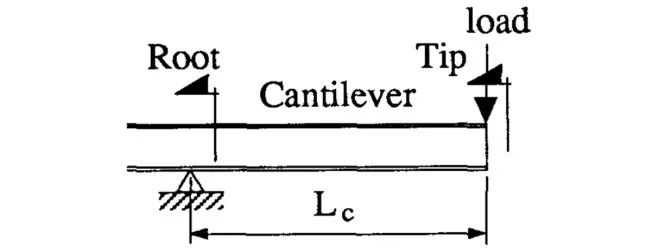
这不正是我们要寻求的答案吗？
应用举例
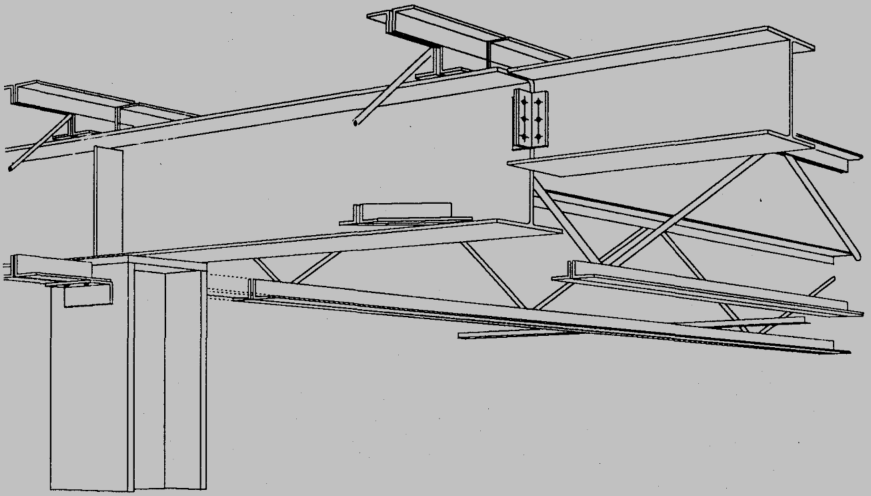
侧向无支撑悬臂梁在工程实际中非常常见，最常见的例子譬如：工业建筑中由建筑物面悬挑而出的悬挑吊车梁，在建筑物内部悬挑梁的backspan位于暖通及机电管道上方并由屋面梁支承，悬挑吊车梁的末端延伸到建筑物外部，以便可以将货物吊起并带入建筑物。提升装置具有在梁的底部翼缘上运行的轮子，因此为了不干扰起重提升装置操作，不能在悬臂梁的底部翼缘上设置任何加强件或支撑。此外建筑师或许不允许在建筑物外部为悬臂梁末端提供侧向支撑。因此在这种情况下，此悬臂梁的末端上下翼缘无任何侧向支撑，悬臂梁只是在支座（root）处有上翼缘侧向约束，此时k应该取3.0.
以下为另一组常见例子及对应的K的取值：
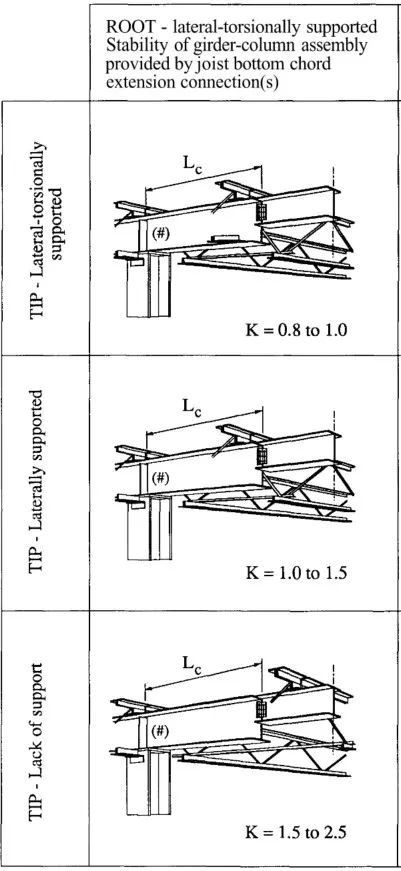
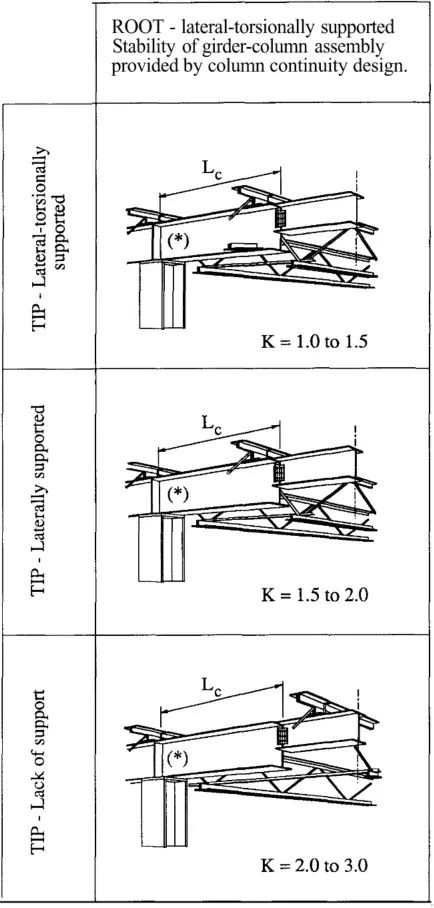
注：
上图中（#）表明梁腹板可以不设加劲肋，如果腹板局部抗压承载力满足要求的话；
上图中（*）表示设置沿梁腹板全高的加劲肋以确保柱承载力连续；
结论和启示
综上比较可知，中国规范和加拿大规范均给出了对于悬挑梁支座为理想固接的情形下的稳定承载力公式，而美国规范未在条文中明确给出。无论是中国规范，还是美加规范，规范正文均未给出对于悬挑梁在不同的支座约束条件下稳定承载力计算公式；因此要想解决这一常见的问题，必须要参考其他相关的技术文献。其中Nethercot的研究成果并为CISC所推荐的补充计算长度系数法为美加转自：中普遍采用的分析方法，其好处是概念上非常简单直接便于理解，同时cover了绝大多数常见的支座条件和荷载情形，并具有合理的安全储备。但是，中国规范在悬臂梁的整体稳定设计公式推导方面有其自身独到的特点，与美加规范体系并不一致，故本文中所提及的补充计算长度系数法是否适用，适用范围以及对设计结果的影响等，建议有兴趣的工程师可结合具体案例进行试算并与美加规范的结果进行比较验证。未对其结果的合理性和安全度有充分认识后不得用于实际工程设计。
-
转自：规范 GB50017 – 2017。 -
AISC 360 -16 Specifcation for Structural Steel Buildings -
CSA S16 -19 Design of Steel Structures -
CISC Roof Framing with Cantilever (Gerber) Girders & Open Web Steel Joists. -
AISC (1999), Load and Resistance Factor Design for Structural Steel Buildings, AISC, Chicago. -
Nethercot, D.A. (1973), “The Effective Length of Cantilevers as Governed by Lateral Buckling,” The Structural Engineer, Vol. 51, No. 5. -
Nethercot, D.A. (1983), “Elastic Lateral Buckling of Beams,” Beams and Beam-Columns: Stability and Strength (ed. R. Narayanan), Applied Science Publishers, Barking, Essex, England. -
Galambos, T.V (ed.) (1998), Guide to Stability Design Criteria for Metal Structures, Structural Stability Research Council, 5th Edition, John Wiley and Sons, New York. -
Kitipornchai, Dux, Richter (1984), “Buckling and Bracing of Cantilevers,” Journal of Structural Engineering, Vol. 110, No.9 -
Salmon and Johnson (1996) Steel Structures—Design and Behavior, 3rd Edition, p. 511, HarperCollins, New York. -
AISC (1999), Manual of Steel Construction, Load and Resistance Factor Design, Third Edition, AISC, Chicago. -
Essa and Kennedy (1995), “Design of Steel Beams in Cantilever-Suspended-Span Construction,” Journal of Structural Engineering, Vol. 121, No.11 -
Bo Dowswell (2004) “Lateral-Torsional Buckling of Wide Flange Cantilever Beams,” Engineering Journal, Vol. 41, No. 2.
（本文完）
喜欢作者文章的朋友可长按二维码订阅作者公众号
▼
如对本文有任何疑问或具体意见反馈，请给后台留言。
如有收获，分享转发 或 点亮“”▼
