“转自:“
钢填板-螺栓节点是现代木结构建筑中最常采用的节点形式,此类节点在设计过程中,为便于安装,钢板及木构件上开设的螺孔往往比螺杆直径稍大,因此,当一个节点安装完毕后,螺栓相对于钢板孔、木孔可能存在间隙。
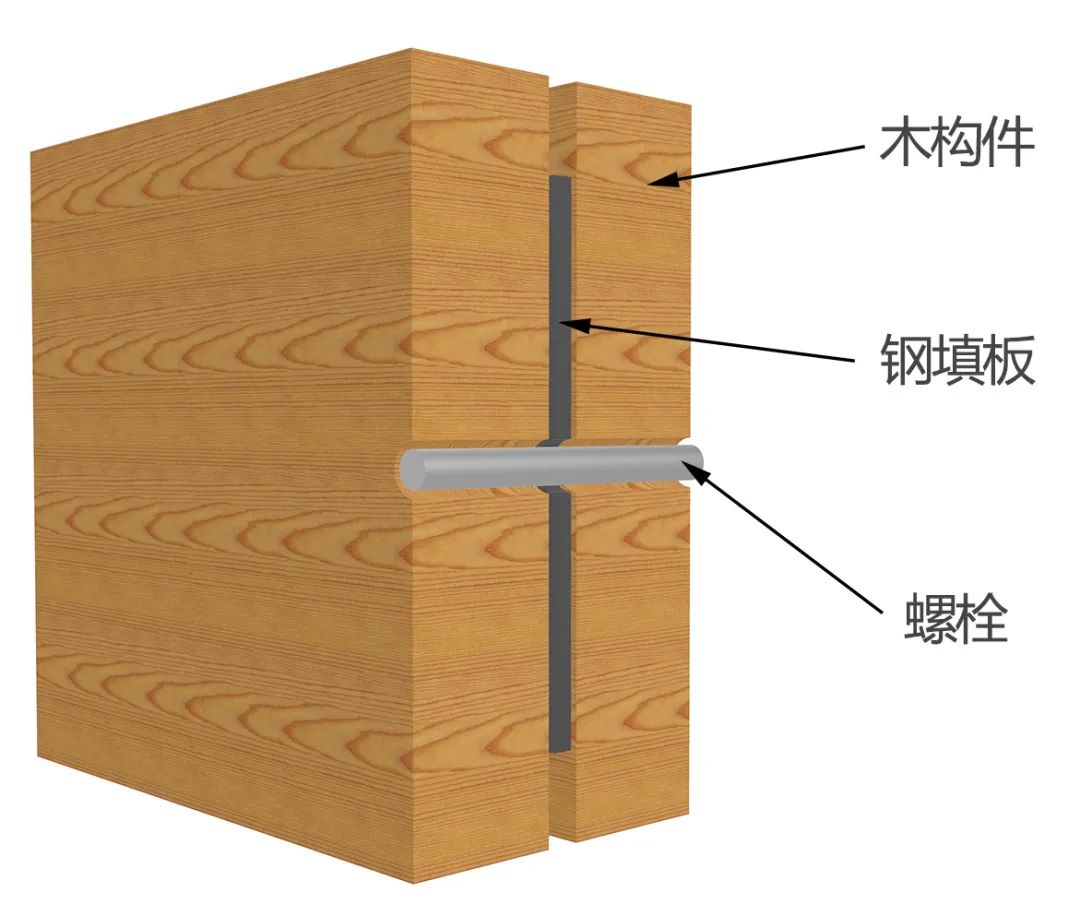
木结构节点的转动刚度对结构承载能力影响显著,近年来一直是业内学者研究的热点。而由于螺栓与螺孔间间隙的存在,节点的转动刚度在初始转动阶段可能趋近于0,随着螺栓与孔壁逐渐压紧,方可发挥节点真正的抗弯能力。
通过总结分析学者们关于钢填板螺栓节点的试验研究,发现钢填板-螺栓节点受弯转动过程大同小异。如下图所示:
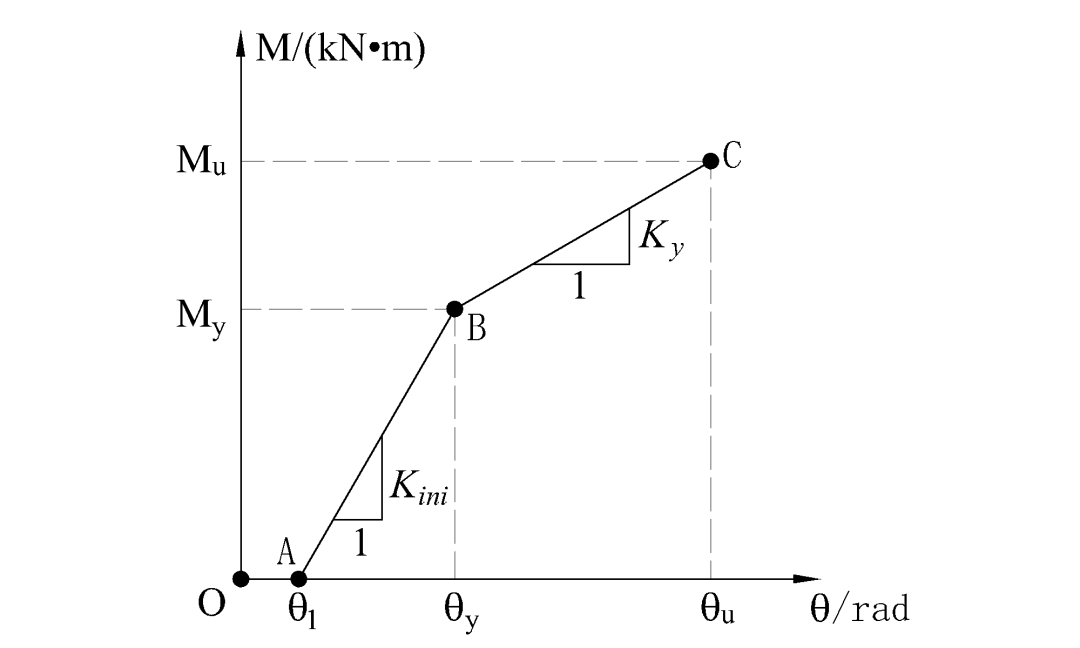
O-A阶段:滑移段,θ1为滑移段极限转角
A-B阶段:弹性段,Kini初始刚度为,θy屈服转角为
B-C阶段:塑性段,Ky塑性段屈服刚度为,θu极限转角为
本篇将针对“钢填板-螺栓节点到底栓紧了没?”即受弯状态滑移段的确定方法及其取值,做以下设想及推演。
1. 螺栓-螺孔相对位置
每一根螺栓安装后可能存在两种状态:
(1) 直径为dt的木孔与直径为ds的钢板孔的交集区域可容纳一个直径为d的螺栓断面,此为螺栓初始未压紧状态,如图1所示。

图1 螺栓初始安装状态
(2) 直径为dt的木孔与直径为ds的钢板孔的交集区域恰好容纳或不可容纳一个直径为d的螺栓断面,此为螺栓初始压紧状态,如图2所示。根据木结构工程经验及销槽承压试验数据,本文通过锤击力与木材销槽承压力的关系,定义螺栓可侵入木材销槽最大深度为1mm,如图3所示。
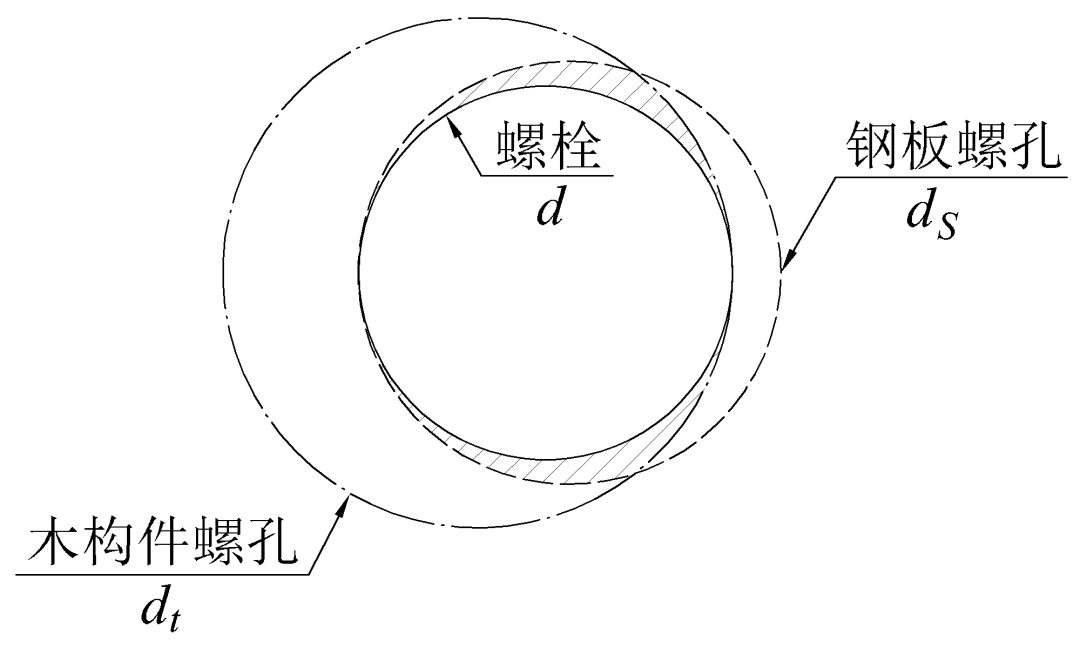
图2螺栓初始压紧状态

图3 木材最大侵入量定义
2. 螺栓-螺孔未压紧概率模型简化
现有任意一个包含n个螺栓的钢填板-螺栓节点,已知该节点螺栓排布为a行×b列,行间距为r,列间距为s,木构件螺孔直径为dt,钢板螺孔直径为ds,螺栓直径为d。螺栓排布如图4所示。
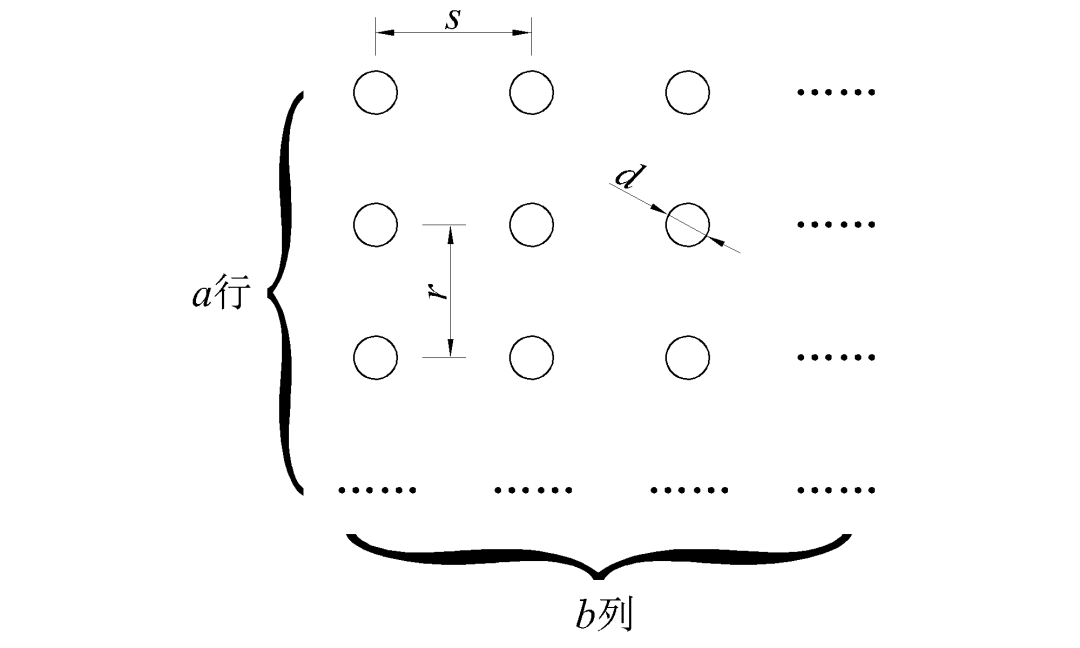
图4 螺栓节点排布
若该节点初始安装状态中至少有一个螺栓与钢板或木构件孔壁挤紧,则可认为该节点已处于压紧状态,即滑移段转角为0。若该节点初始安装状态所有螺栓均处于未压紧状态,设该节点从未压紧状态到压紧状态过程中最大转角为θm,且任意一个螺栓在初始安装状态下未压紧的概率为P,则该节点滑移段转角:
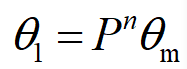
3. 螺栓-螺孔未压紧概率模型求解
3.1 随机概率模型简化
木构件和钢填板在制造过程中存在不可预知的误差,导致木孔与钢板孔存在随机相对位置,包含了螺栓压紧孔壁和螺栓脱离孔壁两种情况,其中任一个螺栓脱离孔壁的概率即为P。前文定义螺栓可侵入木材销槽最大深度为1mm,则木孔与钢板孔位置随机出现的范围是一个直径为Φ=dt+ds-d+1的圆,如图5所示。
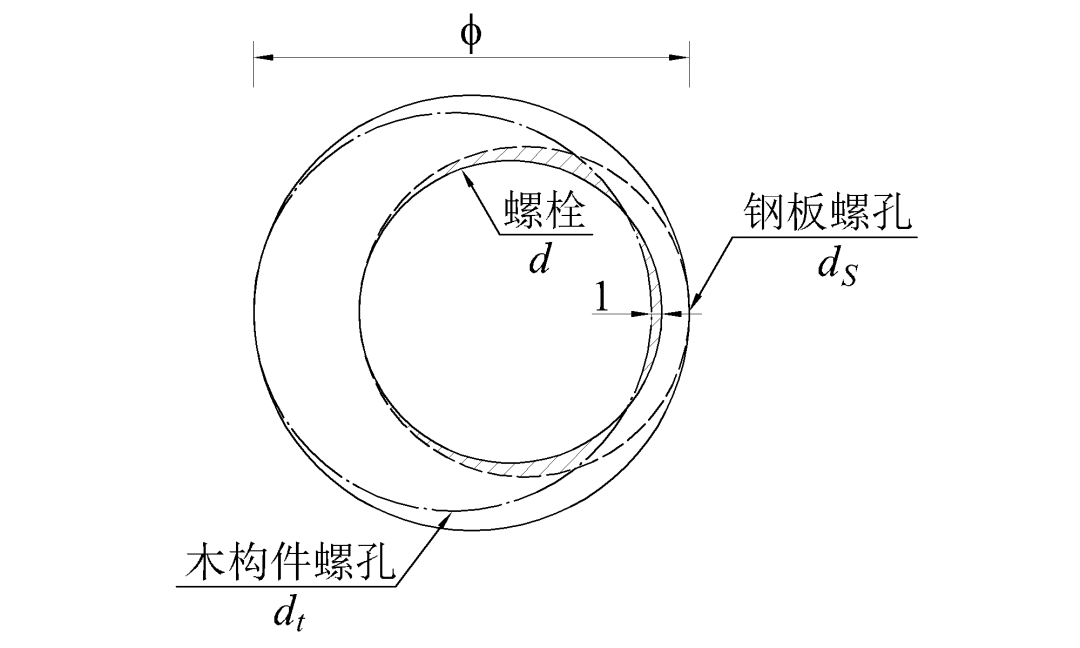
图5 木孔和钢板孔随机位置范围
则该事件发生的概率P可简化为以下模型:
在直径为Φ的圆内随机放置两个直径分别为dt和ds的圆,此两圆交集可容纳一个直径为d的圆的概率。
由于两个圆形随机位置较难求解,可将圆的随机位置转化为点(即圆心)的随机运动,如图6所示,直径为dt的圆在直径为Φ的圆内随机运动,圆心出现的范围是一个半径为R1的圆形。同理,直径为的ds圆在直径为Φ的圆内随机运动,圆心出现的范围是一个半径为R2的圆形。
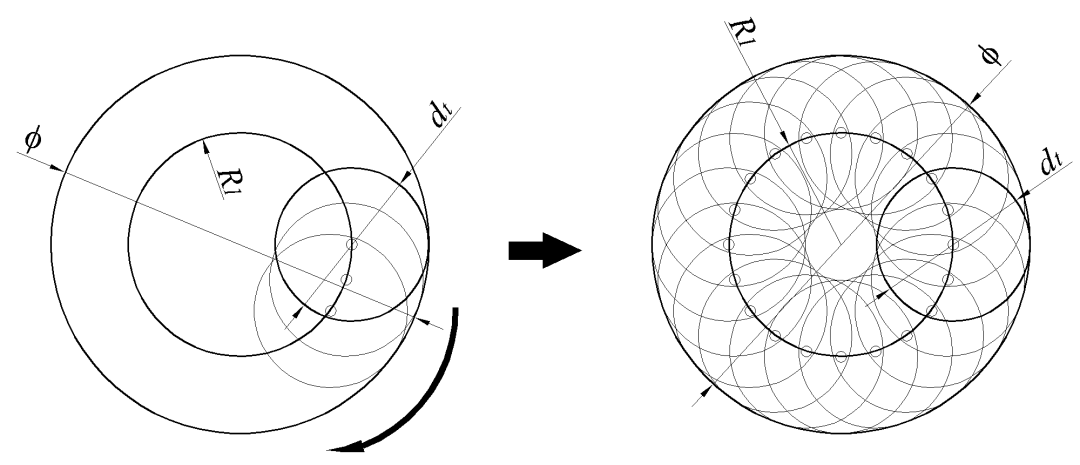
图6 圆心轨迹概率模型
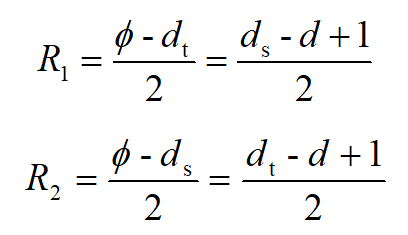
如图7所示,当一个螺栓恰好贴紧木构件螺栓孔和钢板螺栓孔时,两螺栓孔圆心距为q。
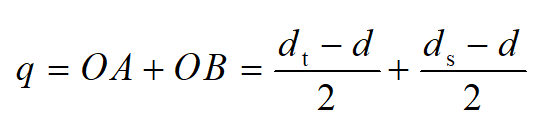
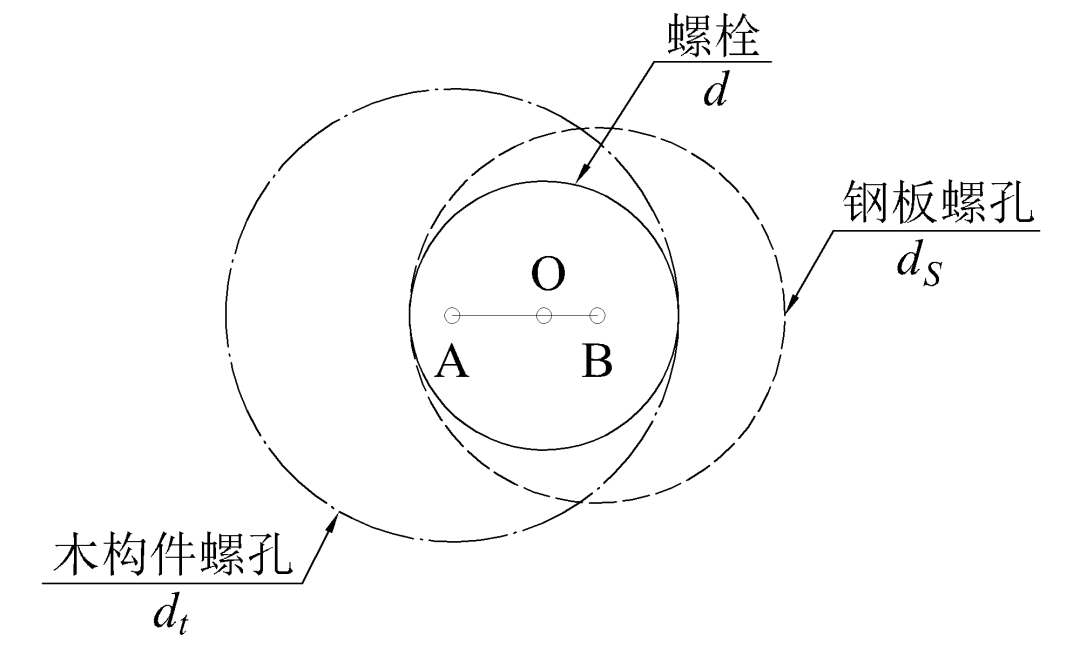
图7 简化概率模型
综上所述,此随机事件可进一步简化如下:
在半径为R1的圆内随机取一点A,在半径为R2的圆内随机取一点B,此两圆为同心圆,线段AB小于q的概率,即:P=P(AB<q)。< p>
3.2 概率公式推导
(1) 当木构件与钢板螺孔直径相等,即R1=R2时,上述事件的特例为:在一个半径为R的圆内随机取两点A和B,AB小于q的概率。
令事件X为:在半径为R的圆内任取一点A,点A落在内外半径分别为x和x+dx的圆环内。
令事件Y为在半径为R的圆内任取一点B,AB<q。< p>
则:
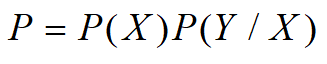
如图8所示,x为在圆内任取一点距圆心的距离,可取微圆环求得事件X的概率:
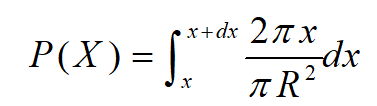
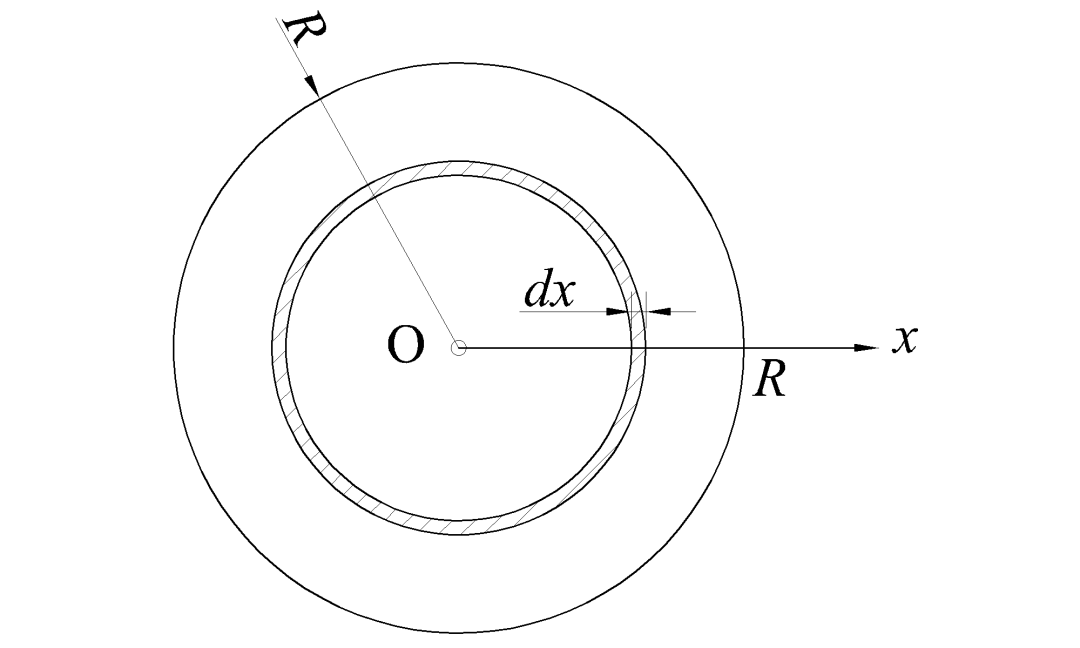
图8 事件X计算模型
① 若R≤q,则第一点A从0到R运动过程如图9所示,在A点确定后B点选取范围为图中阴影面积Sc。
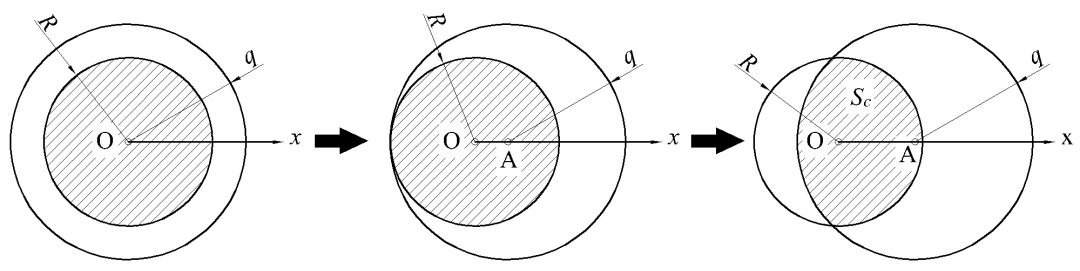
图9 概率P计算模型Ⅰ
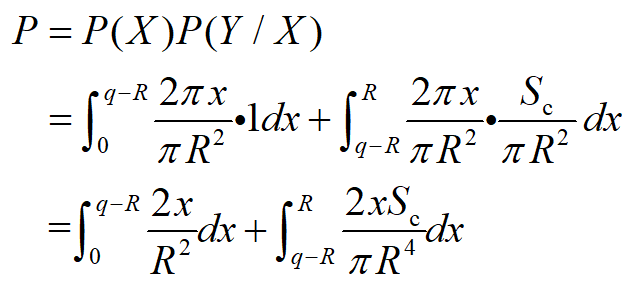
② 若R>q,则第一点A从0到R运动过程如图所示,在A点确定后B点选取范围为图10中阴影面积。
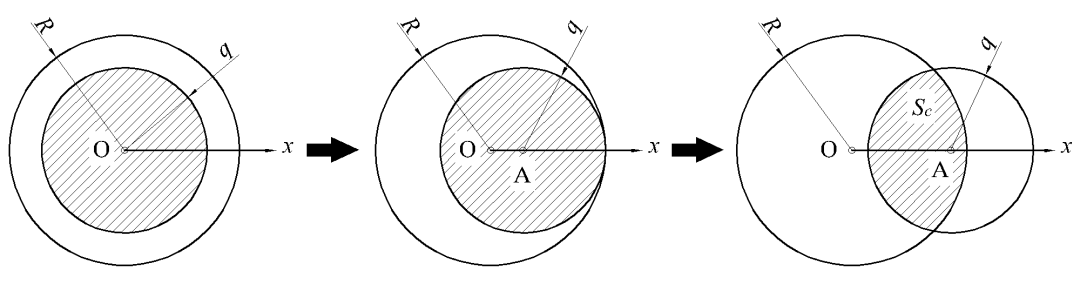
图10 概率P计算模型Ⅱ
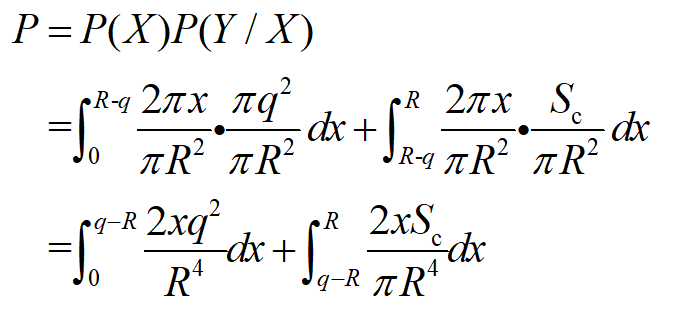
(2) 当木构件与钢板螺孔直径不相等,即R1≠R2时,上述事件为:在半径为R1的圆内随机取一点A,在半径为R2的圆内随机取一点B,此两圆为同心圆,线段AB小于q的概率。
令事件X为在半径为R1的圆内任取一点A,点A落在内外半径分别为x和x+dx的圆环内。
令事件Y为在半径为的同心圆内任取一点B,AB<q。< p>
令R1<r2。
则:
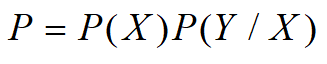
① 当第一点取在半径为R1的小圆内时,事件X的概率为:
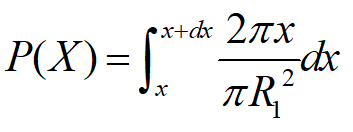
(a) R2<q,则第一点a从0到r运动过程如图11所示,在a点确定后b点选取范围为图中阴影面积sc1。
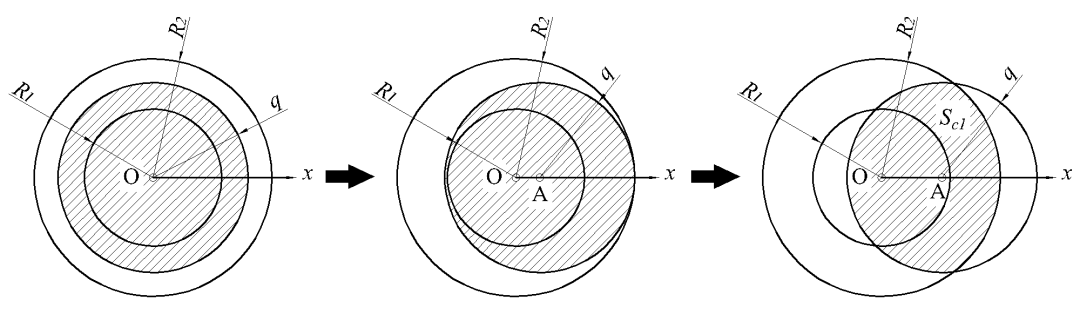
图11 概率P计算模型Ⅲ
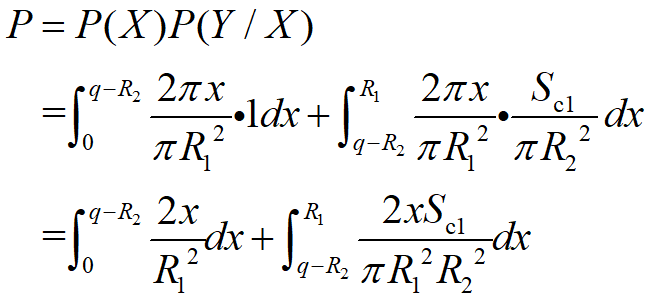
(b) 若R2>q,则第一点A从0到R运动过程如图12所示,在A点确定后B点选取范围为图中阴影面积Sc1。
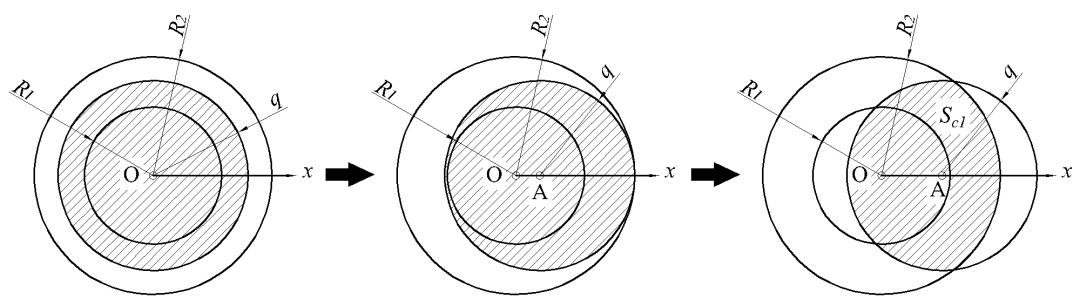
图12 概率P计算模型Ⅳ
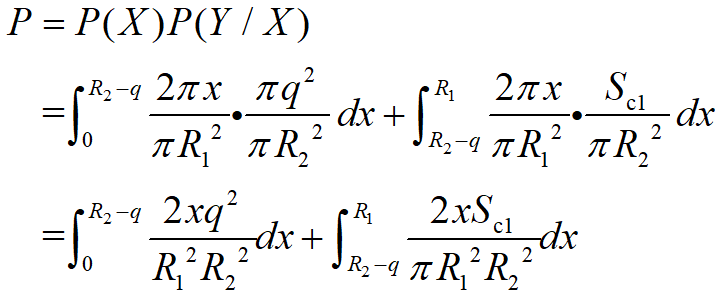
② 当第一点取在半径为R2的大圆内时,事件X的概率为:
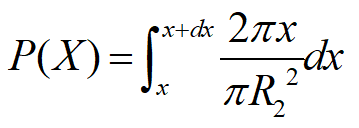
(a) 若R2-R1<q,则第一点a从0到r运动过程如图所示,在a点确定后b点选取范围为图13中阴影面积sc2。
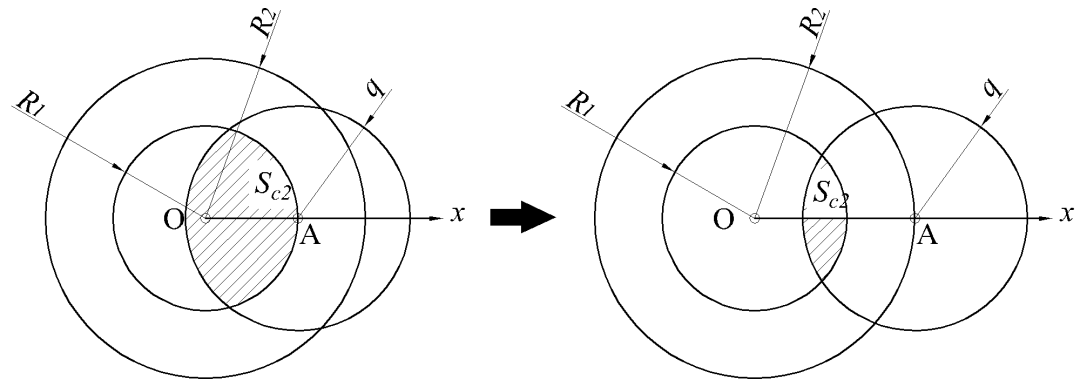
图13 概率P计算模型Ⅴ
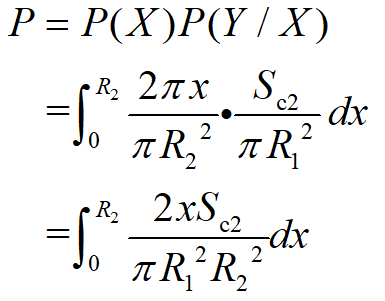
(b) 若R2-R1>q,则第一点A从0到R运动过程如图所示,在A点确定后B点选取范围为图14中阴影面积Sc2。
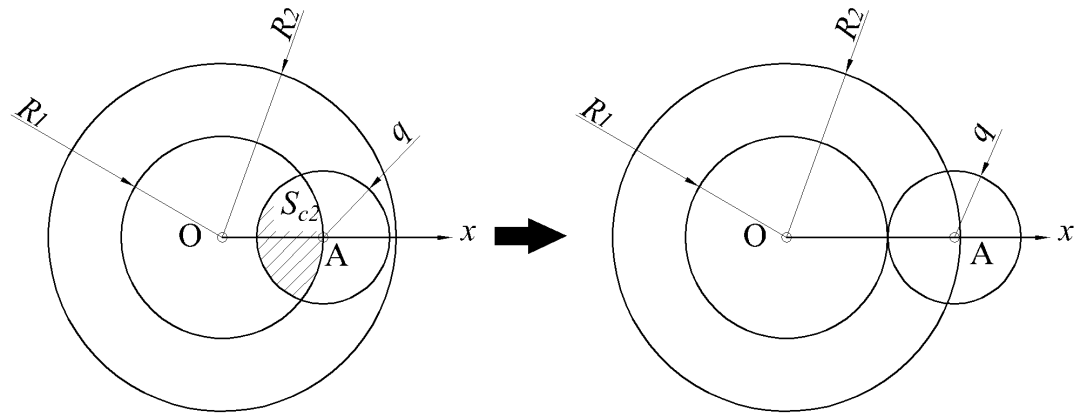
图14 概率P计算模型Ⅵ

综上所述,当R1≠R2时,概率P可分为以上两种情况分别计算。
3.3 概率方程求解
(1) Sc求解
如图15所示,半径为q的圆的圆心A从O点向D点运动过程中可能会出现(a)、(b)、(c)等位置关系,经过简单几何分析发现所有可能出现的情况下:
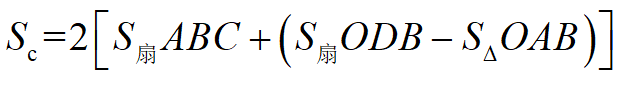
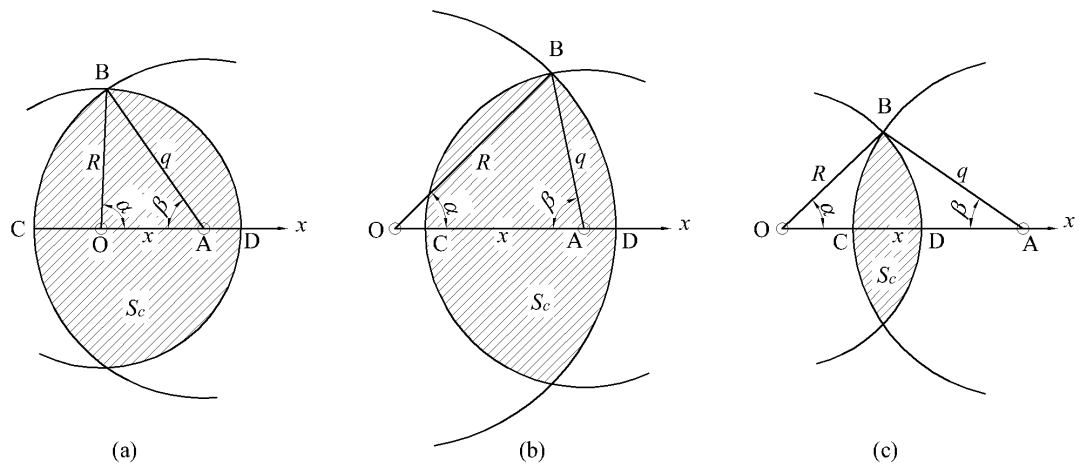
图15 木孔和钢板孔相对位置
又有:
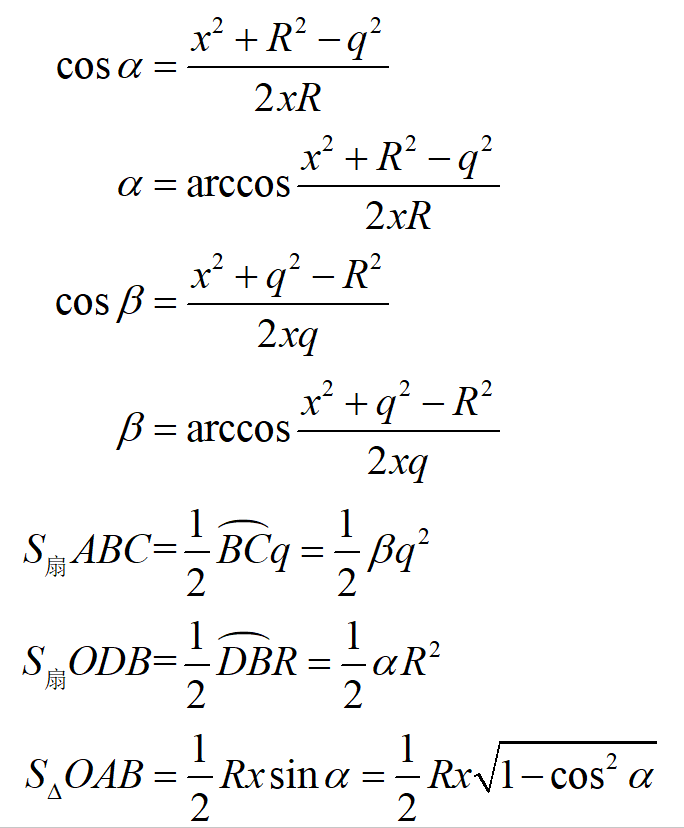
则有:
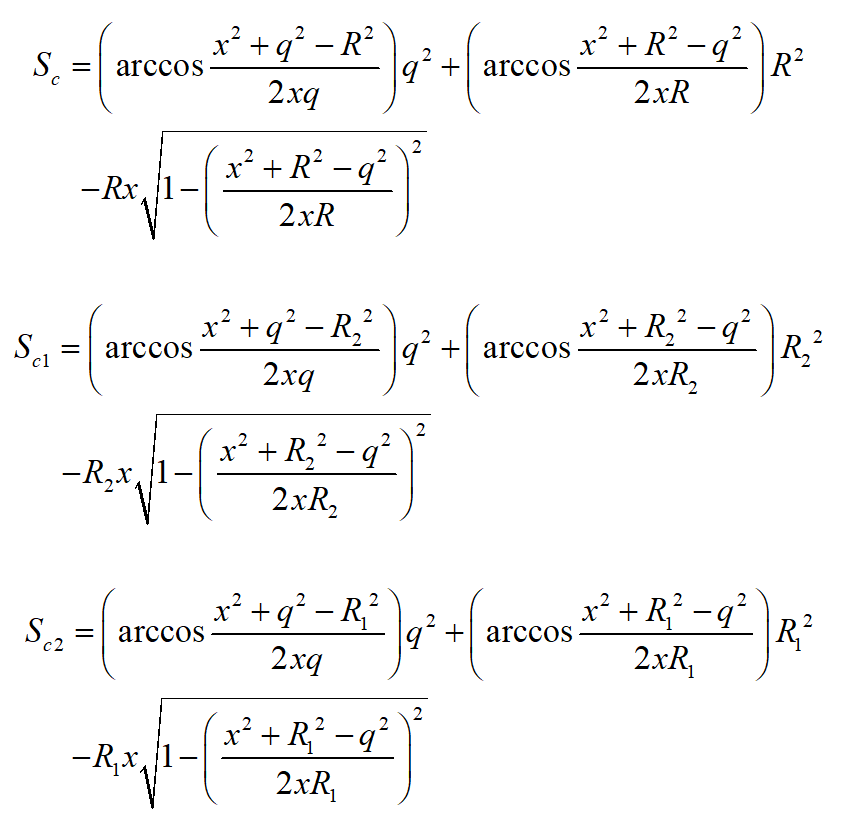
将所求结果分别带入概率方程式即可解得概率积分方程,根据实际设计情况将、、q等参数代入方程即可对其求解。
(2) 确立参数
根据工程设计实际情况,可确立木构件螺孔直径与螺栓直径差值、钢板螺孔直径与螺栓直径差值有可能出现的情况,本文据此给出参数R1、R2、q三种可能取值的情况:
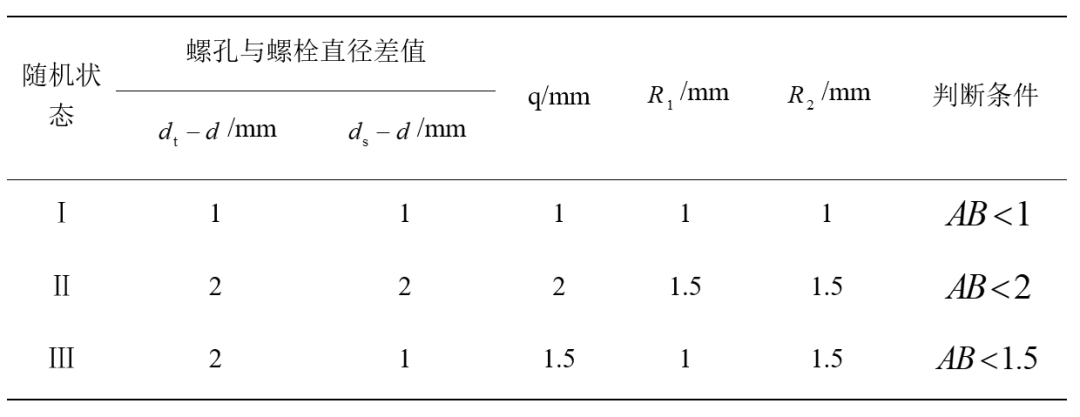
根据前文推导公式,代入各参数,可求得三种随机状态下的概率PⅠ、PⅡ和PⅢ。
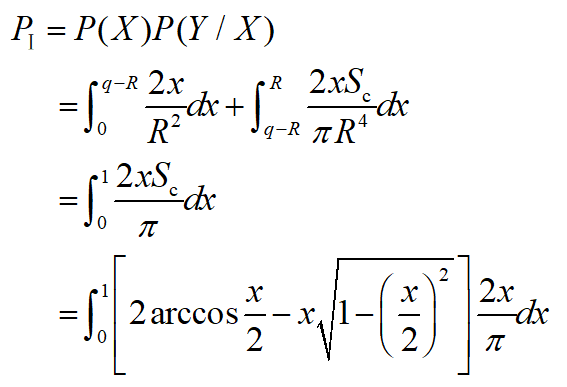
求解可得PⅠ=0.58650
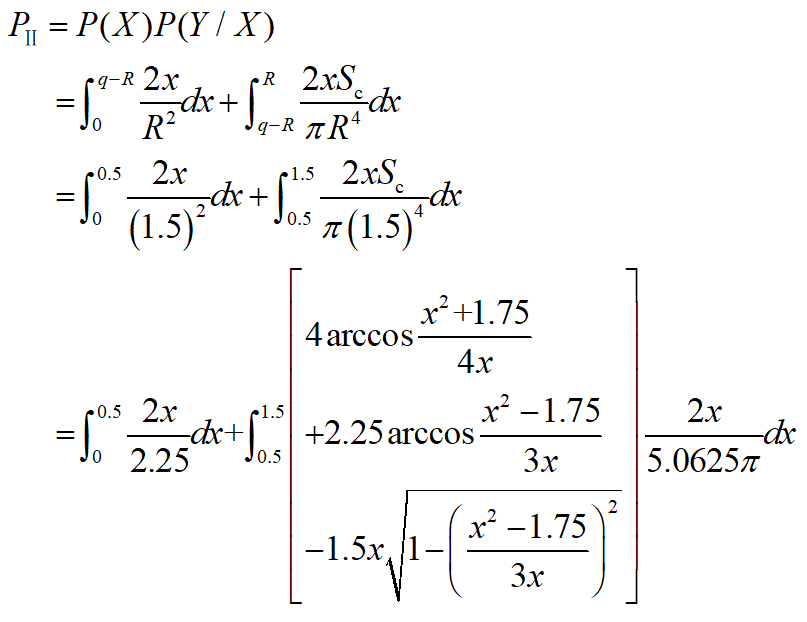
求解可得PⅡ=0.81892
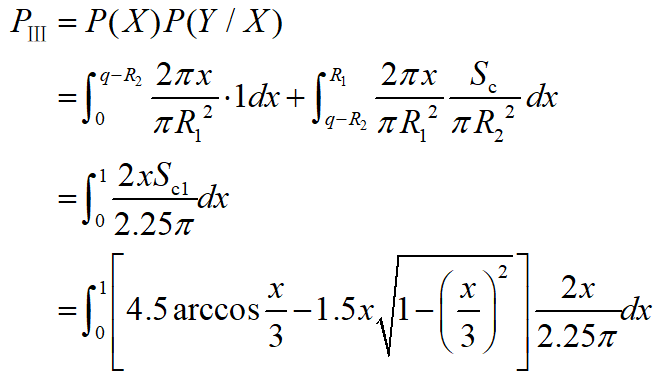
或:
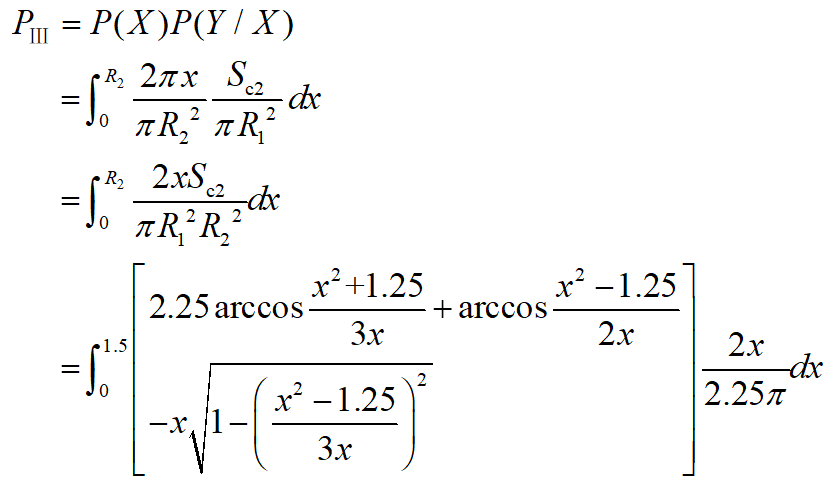
求解可得两种情况解得概率值一致,即PⅢ=0.72024
4. T型钢填板螺栓节点滑移段最大转角
根据几何关系分析,θm,ab为a行b列螺栓排布对角线位置可转动的最大角度,如图16所示,可确定以下参数:
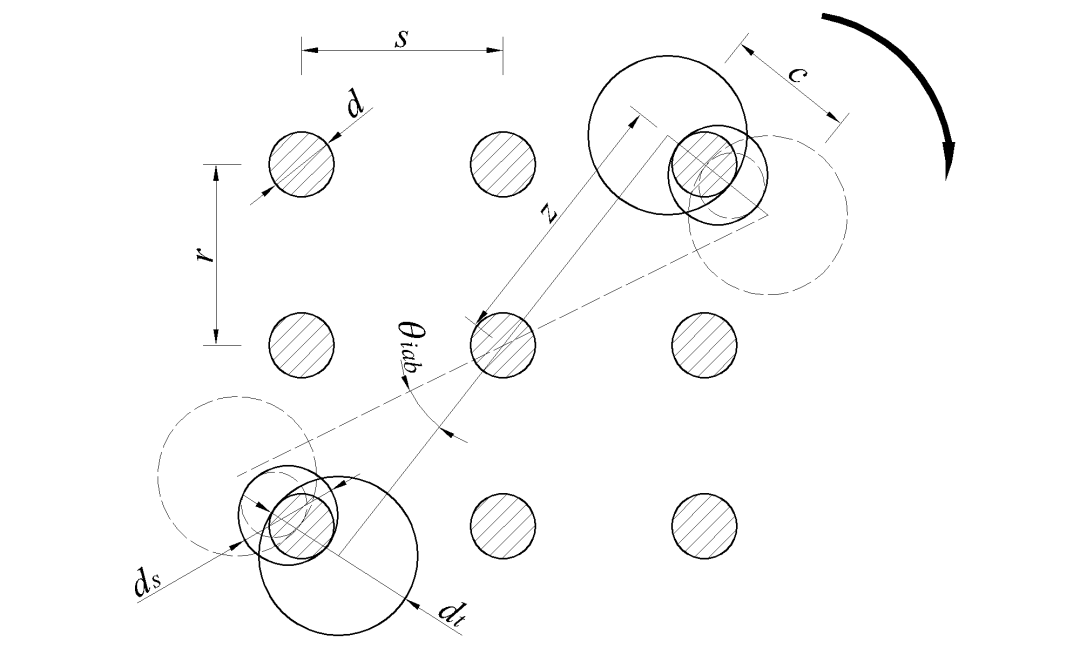
图16 群栓转动示意
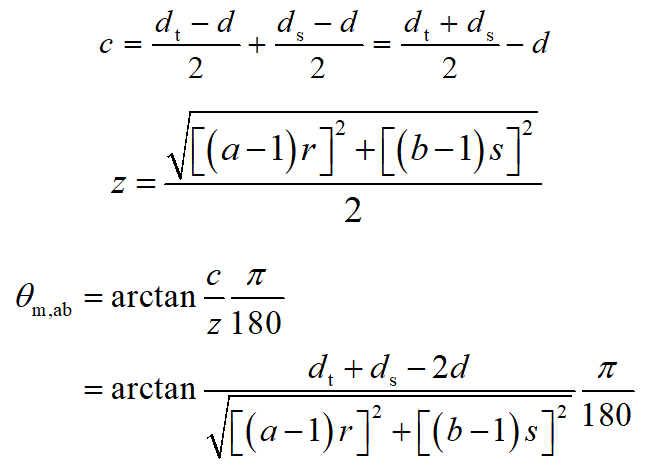
根据本节所推导过程,可确定包含n个螺栓,排布方式为a行b列的木-钢填板螺栓节点滑移段转角为:
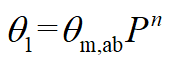
5. 小结
本文重点关注钢填板-螺栓节点受弯转动过程中最初始的滑移阶段。提出了螺栓、木孔和钢板孔的随机概率模型,用以表示任一螺栓安装在群栓节点中任一螺孔时,螺栓与螺孔未压紧的概率。进而将该模型简化为方便计算的数学条件概率模型,对其分类求解,便可得到任一螺栓未压紧的概率。由此概率便可大致评估一个节点在转动滑移阶段的最大转角,进而为更准确的螺栓节点转动刚度计算提供基础。
以上评估及求解方法均为笔者不尽详熟的思路,如有不同见解,欢迎讨论。
参考文献
[1] 王明谦, 顾祥林, 宋晓滨, 等. 胶合木梁柱嵌入钢板-螺栓拼接节点纯弯与弯剪性能试验研究[J]. 建筑结构学报, 2016,37(4):64-72.
[2] 王明谦, 宋晓滨, 顾祥林, 等. 胶合木梁柱螺栓-钢填板节点转动性能研究[J]. 建筑结构学报, 2014,35(9):141-150.
[3] 徐天琦, 马瑜蓉, 宋晓滨, 等. 带翼缘钢填板-螺栓连接胶合木梁-柱节点转动性能试验研究[J]. 建筑结构学报, 2017,38(9):131-137.
[4] 马贵进. 考虑湿度影响胶合木-钢填板螺栓连接力学性能研究[D]., 2015.
[5] Sandhaas C. Mechanical behaviour of timber joints with slotted-in steel plates[J]. 2012.
[6] Pedersen M B U, Clorius C O, Damkilde L, et al. Dowel type connections with slotted-in steel plates: CIB-W18 Timber Structures, 1999[C]. Universitet Karlsruhe.

来源:非解构,如有侵权请联系我们。