我们常用软件显示的构件计算长度等于计算长度系数乘以软件中节点划分的杆件长度，杆件被分割的节点越多，则计算长度系数越大。从这个意义上说，计算长度系数可以很大。

计算长度有个基本前提假定，那就是所有的柱子同时失稳，相关的公式也是按照这个来推导的。当不符合这个假定时，用公式计算的计算长度系数就有误差。

如果一个结构中，各竖向构件的侧向刚度不一样，侧向刚度大的构件会对侧向刚度小的构件提供支撑作用，此时侧向刚度大的构件计算长度系数就会大于按欧拉公式考虑的结果。

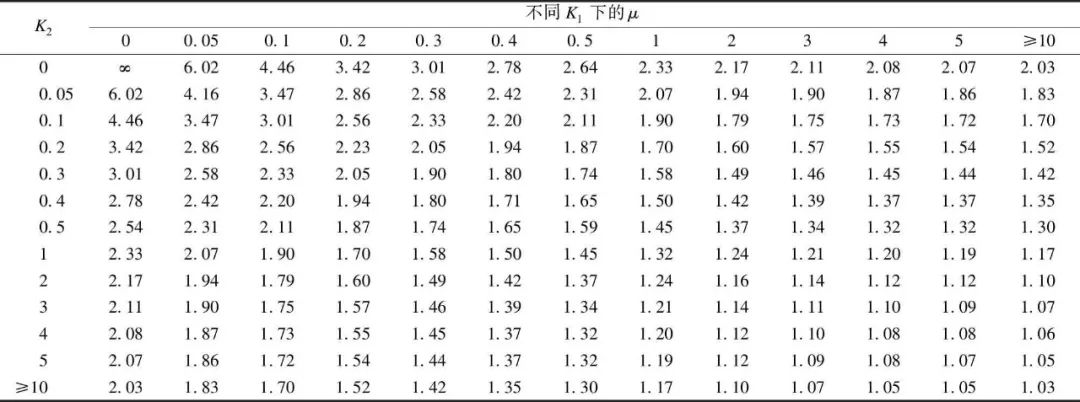
在GB 50017—2017《转自：标准》附录E的表E.0.2有侧移框架柱的计算长度系数中，就有很多计算长度系数大于2.0的情况出现(表1)。表1中的计算长度系数μ值系按式(1)计算得出：

表1 有侧移框架柱的计算长度系数μ

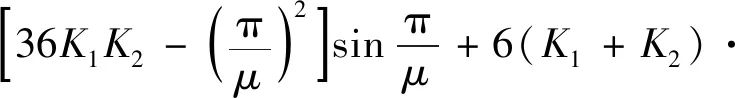
(1)

式中：K₁、K₂分别为相交于柱上、下端的横梁线刚度之和与柱线刚度之和的比值，当横梁远端为铰接时，应将横梁线刚度乘以0.5；当横梁远端为嵌固时，则应乘以2/3；当横梁与柱铰接时，取横梁线刚度为零；对底层框架柱，当柱与基础铰接时，应取K₂=0，当柱与基础刚接时，应取K₂=10，平板支座可取K₂=0.1。

1）PKPM钢柱计算长度系数复核

以图1工程为例，核查PKPM V5.1第二层中柱Z1计算长度系数。钢梁截面均为H500×200×12×18，钢柱截面均为箱形□600×600×20×20，层高4.2 m，钢框架结构，按照一阶弹性分析方法，判定为有侧移框架。PKPM软件输出第二层中柱Z1构件设计属性详见表2。可以看出，此钢柱的计算长度系数为3.02。现手工复核如下。

表2 第二层中柱Z1构件设计属性

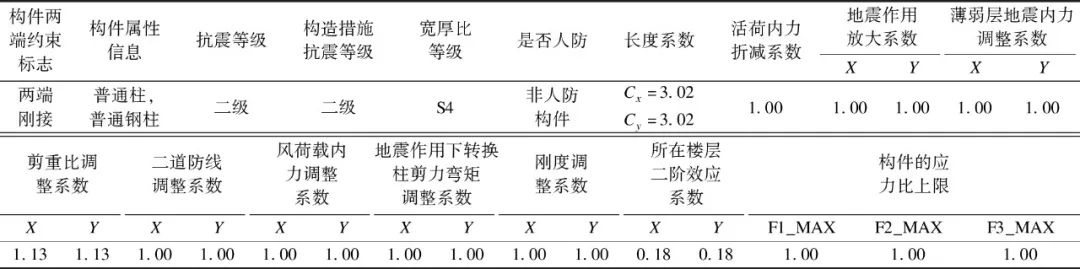
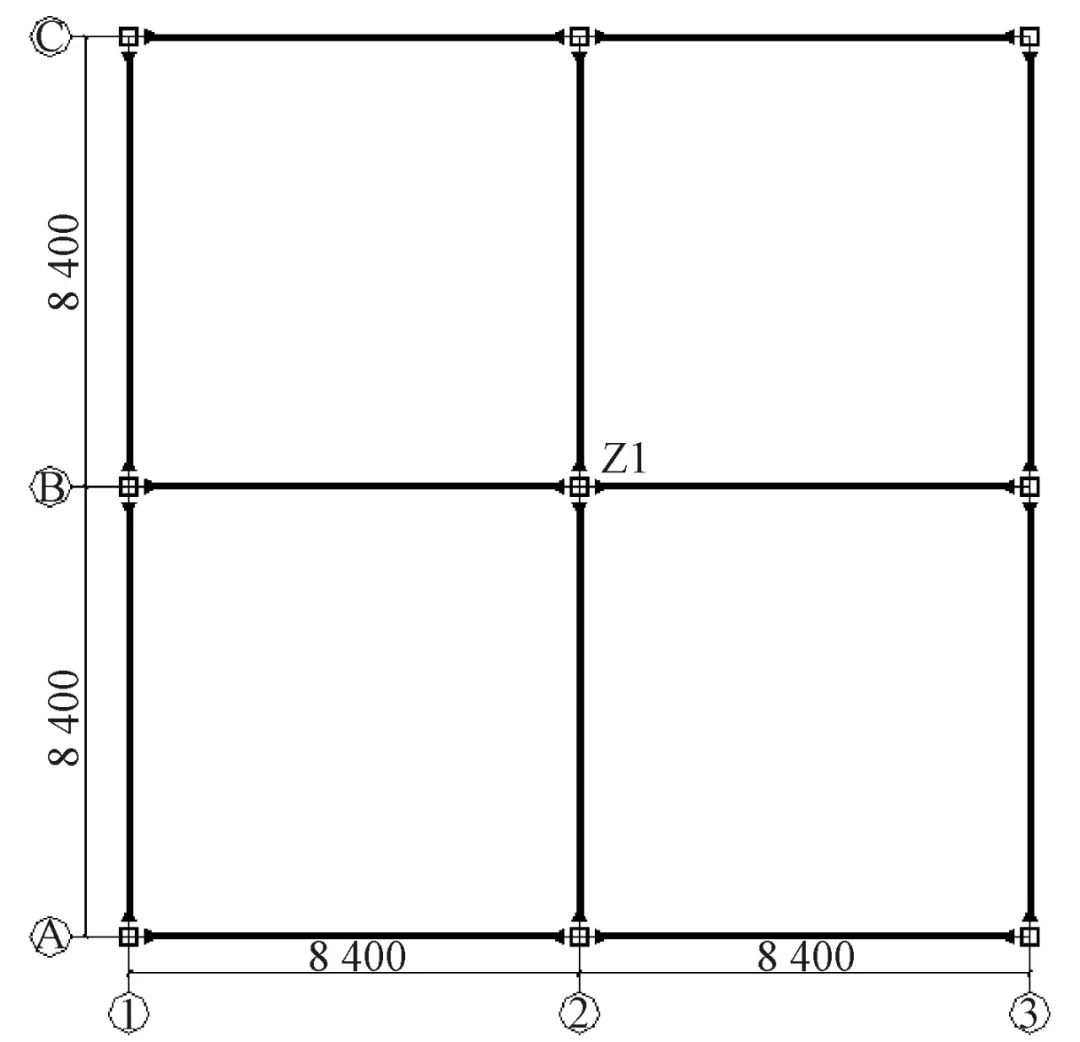
图1 结构平面 mm

第二层钢柱Z1相关梁、柱如图2所示。

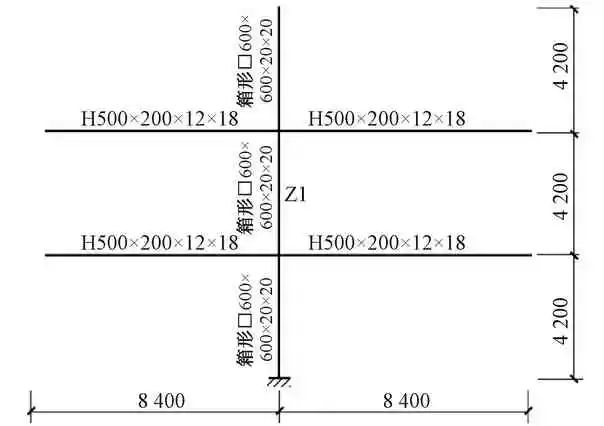
图2 梁柱连接情况 mm

相交于柱上端的柱线刚度之和为：

∑Ic上/lc上=260 458.67/420+260 458.67/420=1 240.28 cm³

相交于柱上端的梁线刚度之和为：

∑I_b上/l_b上=51 827.49/840+51 827.49/840=123.4 cm³

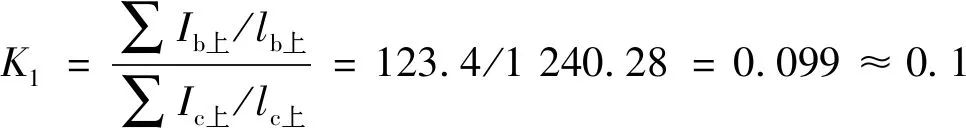
相交于柱下端的柱线刚度之和：

∑I_c下/l_c下=260 458.67/420+260 458.67/420=1 240.28 cm³

相交于柱下端的梁线刚度之和：

∑I_b下/l_b下=51 827.49/840+51 827.49/840=123.4 cm³

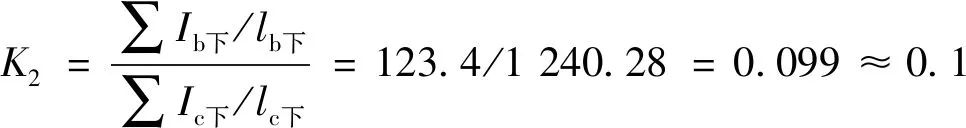
由K₁=K₂=0.1，可查表1得到计算长度系数μ=3.01，其与软件输出结果μ=3.02基本一致。由于程序采用的是精确公式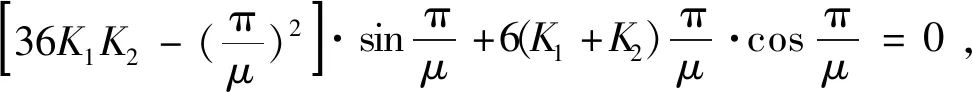应用渐进法求解，手算采用查表及插值结果，可能与程序计算结果稍有差异。

2）三铰静定刚架计算长度系数算例

为什么第二层中柱Z1计算长度系数大于悬臂柱的计算长度系数2.0。陈绍蕃教授在《转自：原理》一书中的论述可以帮助理解这个问题。图3给出一个三铰静定刚架，它的横梁具有较大的刚度，在跨度中央承受一个集中荷载W。当已知W，需要选择柱截面时，对稳定问题不熟悉的设计者在把W分给左右两柱后可能会按两端铰支柱和悬臂柱去选截面，即左柱计算长度为h，右柱计算长度为2h，这种做法显然是错误的。框架在没有侧向支承时，失稳都带有侧移，所以侧移的影响不能忽视。如果认为悬臂柱失稳时上端是有侧移的，不必再另行考虑侧移的影响，也是不正确的，因为没有把框架作为一个整体来考察。下面来分析整个框架失稳而发生侧移Δ的情况。从左柱的平衡看，支点A必有水平力H，其值可由B点力矩和为零得出，即:

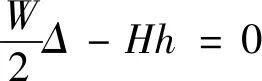
(2)

则：

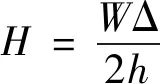
(3)

右柱相应的平衡情况见图3c。

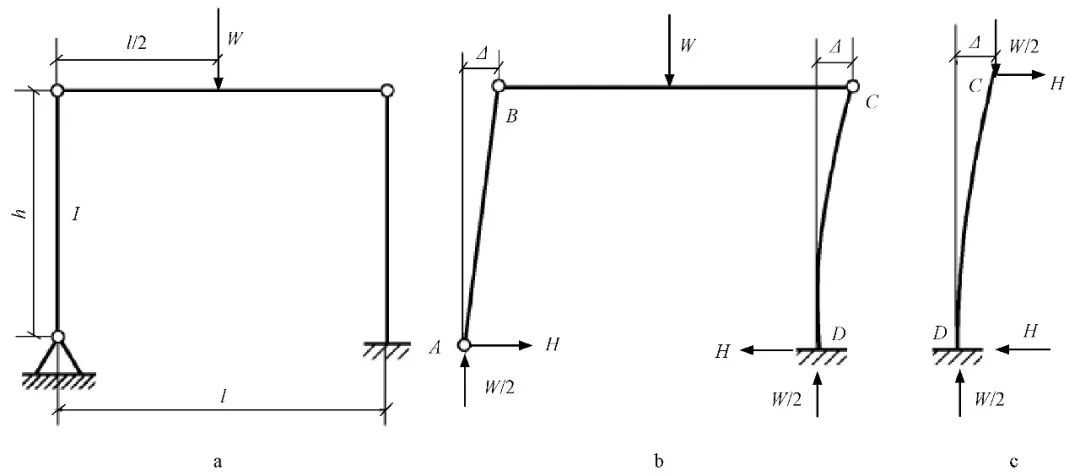
图3 三铰刚架的稳定分析

下面推导同时承受水平力H和竖向力P的悬臂柱顶点侧移(图4)。按照变形后的位形来分析，在小变形范围内柱内任一截面内有：

图4 同时受水平力的悬臂柱

EIv″=-Pv-Hz+M(0)

(4)

由边界条件v(0)=v′(0)=v″(l)=0可以解得:

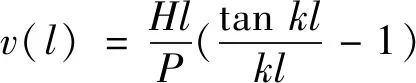
(5a)

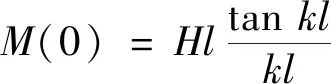
(5b)

其中

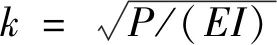
在式(5a)中代入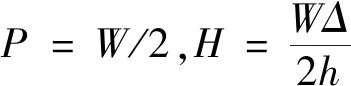和v(l)=Δ，得：

(6)

解得：

kh=1.167

(7)

即：

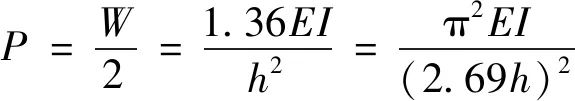
(8)

由以上分析可知，右柱的计算长度应该是2.69h，而不是2h。如果按照2h计算，临界力比实际大了81%，很不安全。悬臂柱的计算长度为什么会大于2h？从整体上看框架的侧向刚度只能由悬臂柱提供，铰接柱毫无抗侧移的能力。因此悬臂柱对左柱上端提供弹性支座的作用，它不仅仅是承受本身的W/2压力，还要包括对左柱的支援作用，这种作用表现在承受水平力H。H和P的合力是一个斜向作用力。悬臂柱的计算长度可以由图5的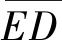来表示，它大于2h。

图5 右柱计算长度

3）三铰静定刚架SAP 2000验证

下面用SAP 2000 V21.2.0验证图3的三铰静定刚架右柱的计算长度系数，跨中施加W=1 kN的恒载，跨度l=6 000 mm，层高h=3 000 mm，柱截面为箱形□200×200×10×10，Q355钢材(图6a)。依靠欧拉公式(9)来获得构件计算长度系数。

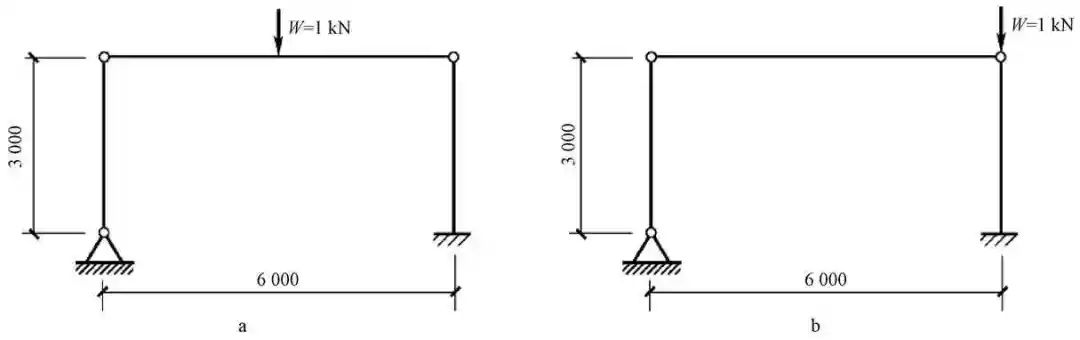
图6 三铰刚架

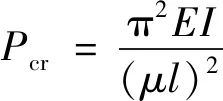
(9)

通常情况下，遵循如下步骤：

1)在施加荷载工况下获得该构件的轴力N；

2)以施加荷载作为激励荷载，运行屈曲工况，获得对应构件屈曲时的屈曲因子λ；

3)计算构件的临界力P_cr=Nλ，然后按式(10)获取计算长度系数μ，其中E为弹性模量，I为截面惯性矩，l为构件几何长度。

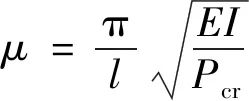
(10)

首先增加屈曲荷载工况(图7)。需要提醒的是，为使软件结果逼近理论上的精确解，还需要进行以下操作：

图7 增加屈曲荷载工况

1)因自重属于恒载，为了剔除自重对柱临界力的影响，需将钢材密度设置为0。

2)欧拉公式的两个基本假定，即仅考虑弯曲变形、挠曲线为三角(正弦或余弦)函数。

默认情况下，SAP 2000 中的框架单元均为铁木辛柯(Timoshenko)梁，根据剪切刚度计算剪切变形；欧拉公式则假定剪切变形为零。为了实现欧拉公式“仅考虑弯曲变形”的假定，可以对框架对象或框架截面指定属性修正系数，将沿②轴和③轴的剪切面积的修正系数设置为零即可。

另外，SAP 2000中框架单元的插值函数为三次函数，而欧拉公式采用三角(正弦/余弦)函数的挠曲线。因此，单个框架单元的变形曲线无法精确拟合欧拉公式采用的挠曲线，需要对框架对象进行适当的剖分(本算例将构件自动剖分选项中最少剖分数量指定为10)，则可以无限逼近理论上的精确解。

3)忽略结构平面外失稳。在“分析选项”对话框中点击“平面框架-XZ平面”按钮，快速选择有效自由度U_X、U_Z和R_Y。

4)忽略杆件轴向变形。对构件进行属性修正，横截面面积放大10 000倍。

屈曲分析的前三阶结果见图8，第一阶屈曲因子λ为2 768.589 86。在W=1 kN荷载下，右柱轴力N=0.5 kN。故临界力为：

P_cr=Nλ=1 384.294 93 kN

图8 荷载在跨中时屈曲分析的前三阶结果

计算长度系数：

该值与理论上的精确解完全一致。

如果将集中荷载W=1 kN移至右柱顶(图6b)，屈曲分析的前三阶结果见图9，第一阶屈曲因子λ为2 514.192 47。在W=1 kN荷载下，右柱轴力N=1 kN，则临界力P_cr=Nλ=2 514.192 47 kN，计算长度系数这与悬臂柱理论上的精确解完全一致。

图9 荷载在右柱柱顶时屈曲分析的前三阶结果

钢构件计算长度系数的确定，不能仅考虑构件本身，还应综合考虑与之相连的其他构件对其的影响。因此，钢柱计算长度系数是可以大于2.0的。