“转自:“
01 背景简介
屈曲是结构或构件的一种失效模式,表现为材料处于正常应力水平时结构整体或局部发生失稳破坏,工程结构中最为常见的是压屈失稳,如下图中的细长压杆、薄壁水箱和混凝土柱。


图片来源:知乎
从数学上来讲,结构在静载作用下出现屈曲(失稳)可以归结为平衡方程的多值性问题,如图所示,在某一负载时出现了一个分叉点和多个解决方案,如果承载力得以继续增加,是最有利的情况,但也有可能沿易变和中立的路径发展,在现实生活中,当然只存在一种路径,将由能量最小化准则来决定。使用传统线性理论计算的解通常不是首选解,或者说,在分叉点附近(失稳临界荷载),任何微小扰动都有可能使结构往失稳的方向发展。
工程设计中当然不允许这种不确定性存在,因而屈曲分析的主要作用就是研究结构在特定荷载下的稳定性以及确定结构失稳的临界荷载,从而保证结构或构件处于稳定状态。
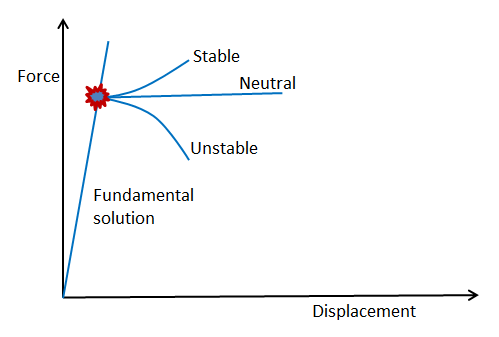
图片来源:正脉CAE博客
02 ABAQUS屈曲分析方法概述
线性屈曲分析(buckle):主要用于对缺陷不敏感结构进行临界荷载和屈曲模态的评估,但无法查看后屈曲状态。
非线性屈曲分析(static,riks):主要用于评估临界荷载以及后屈曲状态,其求解用弧长量代替时间量,可用于对缺陷敏感结构进行带初始缺陷的屈曲分析,但如果结构中存在接触,易出现收敛性问题。
通用静力分析,阻尼稳定(static,stabilize):可以计算结构刚度不变或增大的结构,在静力分析中加入阻尼,有助于收敛,如果结构出现屈曲或突然垮塌,容易出现收敛性问题。
隐式动力分析(dynamic):将屈曲问题作为隐式动力问题来处理,适合接触脱开的问题,但假如模型中的接触对较多,容易出现收敛性问题。
显示动力分析(dynamic,explicit):将屈曲问题作为显式动力问题来处理,能够适应复杂的模型和接触对,收敛效果好,但计算量大、耗时长,计算完成后需要评估结果是否可靠。
今天主要介绍最为常用的前两种求解方法。
线性屈曲分析*Buckle
在ABAQUS中,基于buckle分析步的线性屈曲分析被称为特征值屈曲预测(Eigenvalue buckling prediction),基本分析流程如图所示:
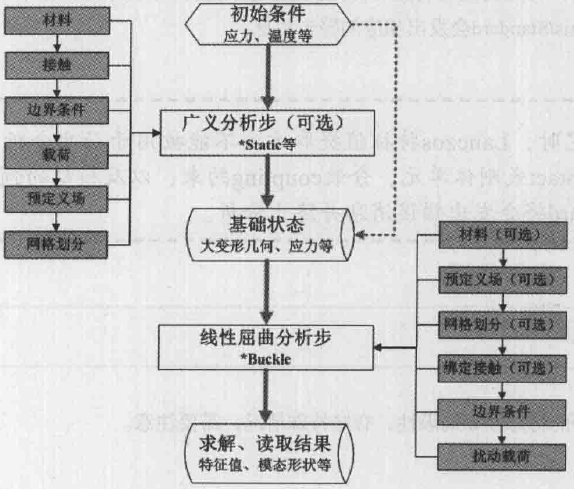
图片来源:《ABAQUS工程实例讲解》
可以看出,在进行buckle分析步之前,可按需进行通用分析步,以获得合适的模型基础状态, ABAQUS在计算特征值屈曲问题时会考虑预加载的荷载刚度,因此必须保证预加荷载不能超过临界屈曲荷载。
在通用分析步中也可以使用非零边界条件预加载结构,但非零边界应用在特征值屈曲分析中将会影响应力增量和微分初始应力刚度,必须小心检查特征值分析结果。在特征值提取过程中,非零边界将被作为约束条件,从而可能影响模态形状,除非设置边界条件为屈曲模态计算,即在Load模块中定义边界条件适用于应力扰动、屈曲模态或二者皆有。
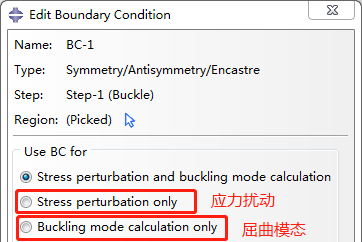
buckle分析步中提供了两种特征值求解方法,Lanczos和Subspace迭代,当要求解的特征模态少于20个时,采用Subspace迭代计算更快,并且当刚度矩阵不确定,比如模型中包含连接单元、接触单元、分布式耦合约束等时,Lanczos方法将不能适用。
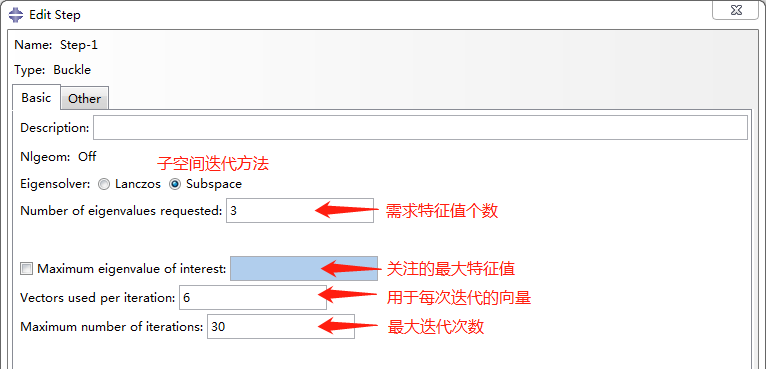
在特征值屈曲分析步中施加的荷载仅用以表现线性扰动,其值大小并不重要,屈曲临界荷载=特征值×施加荷载值。此外,特征值屈曲分析中模型的响应是基于基础状态的线弹性刚度,故所有非线性/非弹性的材料属性都将被忽略。
非线性屈曲分析*Riks
相对于线性屈曲分析,非线性屈曲分析可以考虑几何、材料和边界条件等非线性行为,ABAQUS中称为不稳定倒塌和后屈曲分析(Unstable Collapse and Postbuckling Analysis),基本分析流程如图所示:
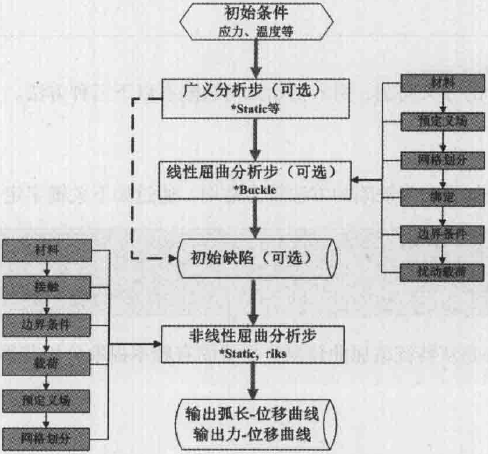
图片来源:《ABAQUS工程实例讲解》
采用riks法求解后屈曲问题时,必须将上面提到的屈曲时的求解分叉问题转化成连续响应问题,一般采用引入初始缺陷的办法,如此使得临界荷载达到前,屈曲模态就有一定响应。初始缺陷可分为几何缺陷以及荷载缺陷,对于几何缺陷,除非已知缺陷的精确形状,一般都采用前几阶(线性)屈曲模态叠加而成;而荷载缺陷,也应该在期望的屈曲模态下扰动结构,如下图所示:
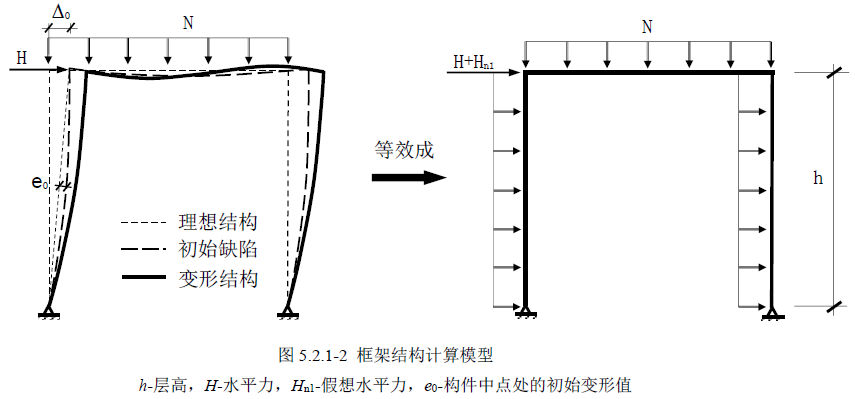
图片来源:《转自:标准》GB50017-2017
Riks分析步选项卡中各参数含义释义如下:
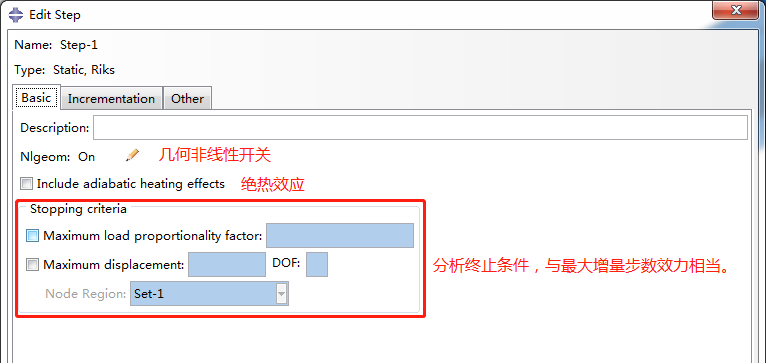
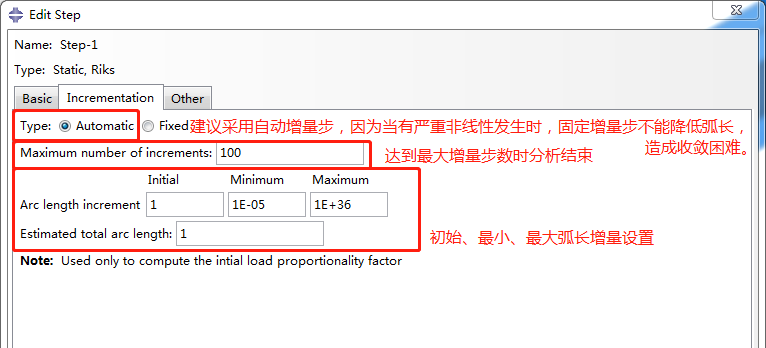
03 案例练习
对于下图所示的H型钢柱,首先进行线性屈曲分析,输出屈曲模态,用作后续非线性屈曲分析的初始几何缺陷,比较二者计算得出的屈曲临界荷载,以及进行缺陷敏感性分析。

H型钢柱的截面为420×300×12×20mm,高5m,采用壳单元模拟(S4R),钢材使用弹塑性本构,参数如下。
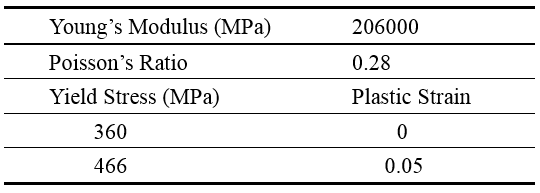
建模、装配、网格划分等步骤同一般静力学分析,不再赘述,在Step模块,分析类型选择“Linear perturbation: Buckle”,请求特征值个数设置为3,其余默认。在Load模块,设置参考点耦合柱顶部壳边,并对参考点施加1kN的集中荷载(压力)。
因为后续分析要用到Buckle求解的屈曲模态作为初始缺陷参考,故需要添加关键字来定义输出屈曲变形位移的需求,在 *End step之前插入关键字:
*NODE FILE, GLOBAL=YES, LAST MODE=1
U
即只输出最低阶模态形状(节点位移),计算完成后可以在工作目录下找到Job.fil文件,即为该节点位移文件。
这里额外讨论,《钢标》5.2节对于结构整体初始几何缺陷和构件的初始缺陷都提出要求,如图。对于结构整体初始缺陷,规范建议可按最低阶整体屈曲模态取用,但有研究认为对于某些缺陷敏感性结构,屈曲后屈曲模态相互影响作用较大(表现为各阶屈曲特征值间隔很近),基于单一屈曲模态作为初始缺陷往往会产生非保守的结果,此时可以通过调整各个屈曲模态的比例因子大小,调整缺陷大小,再执行不同缺陷幅值的分析以获得最不利的情况。小编认为规范这里作统一规定还是从易操作性出发,毕竟如何确定各模态的比例因子以获得最不利情况比较复杂。
而对于构件的初始缺陷,规范建议采用假想均布荷载进行等效简化计算,并规定了跨中处缺陷代表值的大小,此法应当是各构件屈曲模态未知时的简化算法,毕竟各构件在特定荷载作用下的屈曲模态并非一定如此,当有构件的线性屈曲分析结果时,还是应参考其屈曲模态,因为屈曲模态形状的初始缺陷对结构的稳定性最不利,这是一种较为保险的做法。
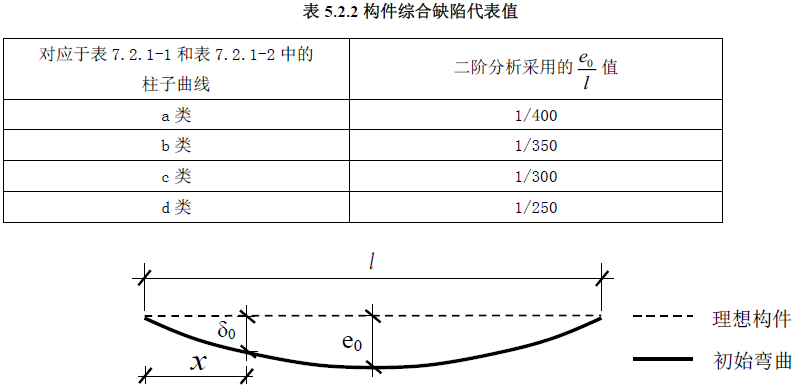
图片来源:《转自:标准》GB50017-2017
Buckle分析结果如下:
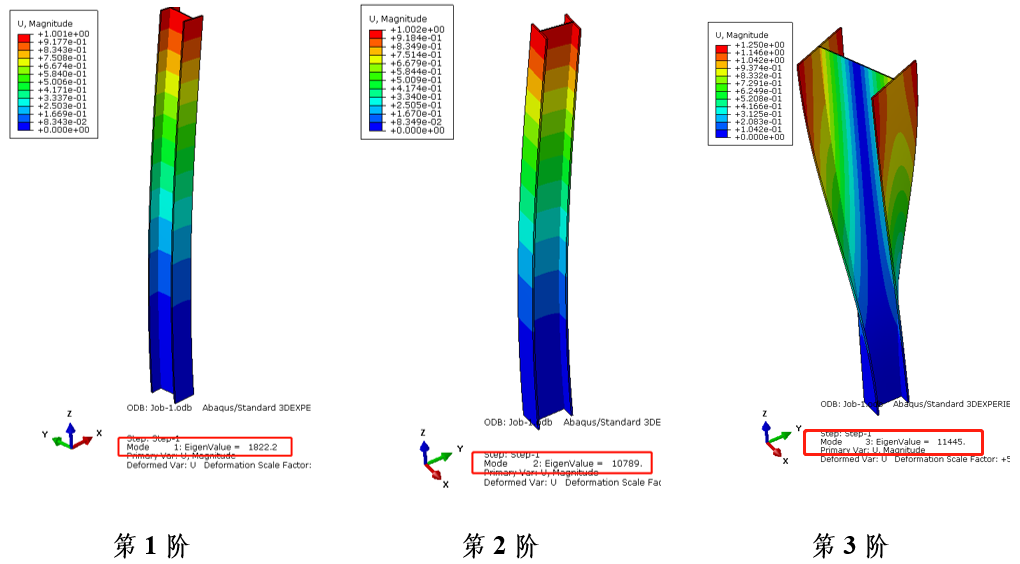
从图中可知在轴心受压情况下,H型钢柱第1阶屈曲模态为绕Y轴(弱轴)的弯曲屈曲,第2阶屈曲模态为绕X轴(强轴)的弯曲屈曲,第2阶屈曲模态为绕Z轴的扭转屈曲,前三阶特征值分别为:1822.2、10789、11445。各阶特征值间隔较大,表示临界力对初始缺陷不敏感,后续分析只参考最低阶模态形状是合理的。
可求得临界屈曲荷载=λ1×F=1822.2kN,而由临界力欧拉公式计算临界屈曲荷载为:
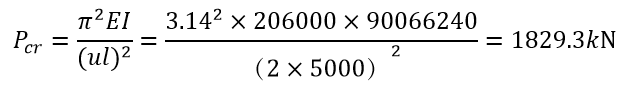
注:因第1阶屈曲模态为绕Y轴的弯曲屈曲,故I取,对于底部固支,顶部自由的钢柱,计算长度系数u取2。
可见buckle方法求解出的临界屈曲荷载与欧拉公式结果十分接近,经验证可靠。
复制该模型,在step模块将buckle分析步替换为“General:Static,Riks”分析步,打开几何非线性,分析终止条件中最大荷载比例系数设为20,弧长增量依次输入:0.1,1E-005,1,其余默认。然后编辑关键字引入初始几何缺陷,在*Step,name=分析步名称,nlgeom=YES之前插入如下关键字行:
*IMPERFECTION, FILE=线性分析作业名称, STEP=1
1, 20
即引入上述buckle分析结果第1阶屈曲形状的20倍作为初始几何缺陷,需要说明的是:buckle分析将位移结果进行了归一化处理,即屈曲模态的最大位移为1mm,故20倍屈曲模态即引入最大点位移为20mm,约为H/250。
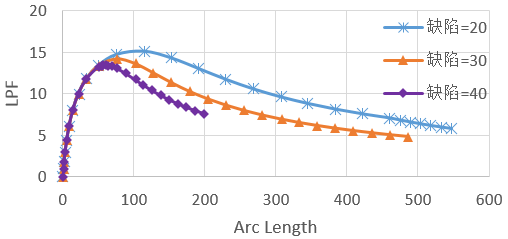
此外在load模块修改加载为100kN(主要为减少计算时间,不影响结果)。Riks分析求解完成后可在历程输出里绘制LPF-Arc length(荷载比例系数-弧长)曲线,如图所示:
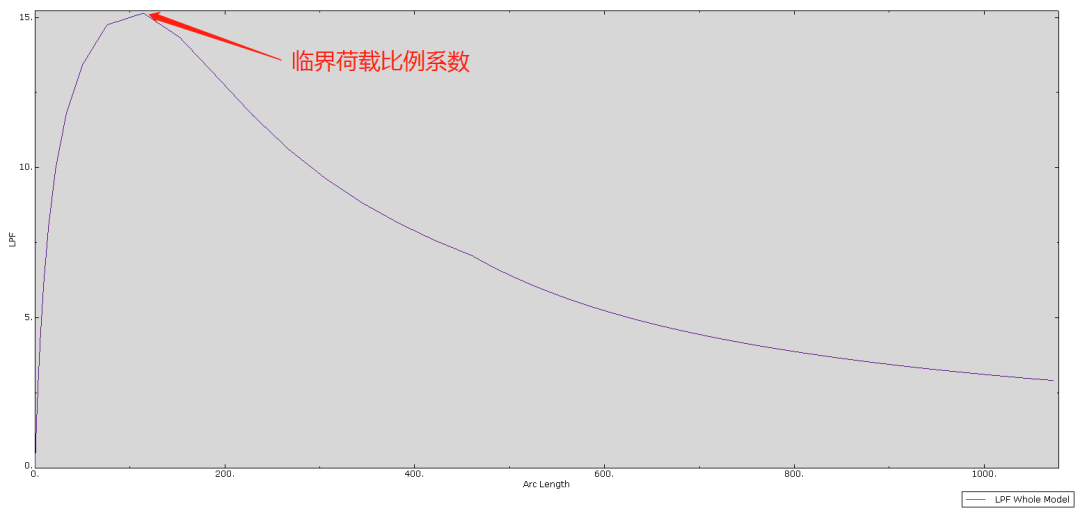
可知曲线第一次转折在Arc length=114,LPF=15.144处,即表明荷载为15.144×100kN=1514.4kN时钢柱发生第一阶非线性屈曲,可见考虑了材料、大变形等非线性情况后,临界非线性屈曲荷载比线性屈曲荷载(1822.2kN)要小,即更易失稳。
把*IMPERFECTION关键字中的缺陷因子分别修改为30、40,重复求解后得到如图所示的不同缺陷因子时LPF曲线,由图可知初始缺陷越大,LPF越小,但对于本例,屈曲临界力对缺陷不是特别敏感(临界荷载比例系数随缺陷增加而下降不多)。
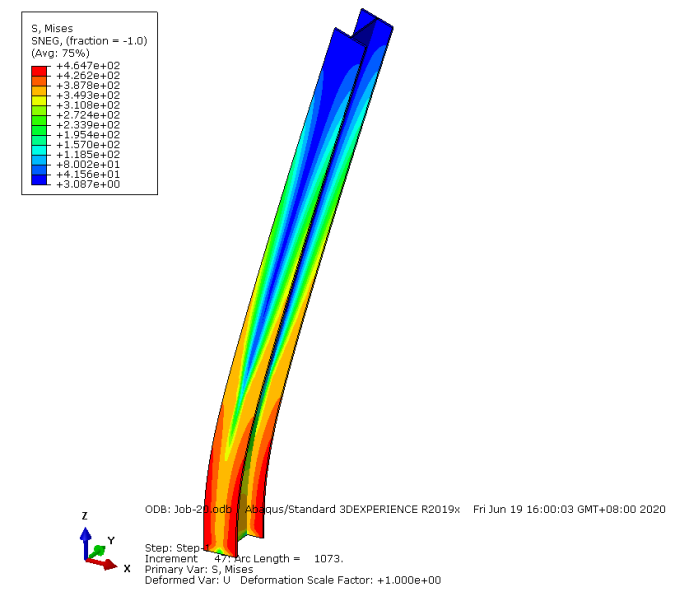
此外,riks非线性屈曲分析还可以展示结构的后屈曲形态,如图所示为20倍模态缺陷、弧长增量=1073时,钢柱的屈曲形态:钢柱在屈曲后持续受荷,绕其弱轴压屈进一步发展。
04 注意事项
(1)特征值屈曲分析(buckle)中,有时会出现负特征值,表示相反方向的荷载造成了屈曲,比如由于刚性体的局部屈曲,外部压力下的容器可能出现负特征值,即内压屈曲。
(2)特征值屈曲分析理论是依赖于屈曲荷载引起的微小变形,大变形可在预加载中形成,如果屈曲荷载步中产生了大变形,就必须应用非线性的riks分析。
(3)Riks算法不能得到特定荷载或位移处的结果,如需获得精确荷载、位移处的结果,需要在分析步的期望点重启动以定义一个新的非riks分析步。
(4)对于涉及接触失效的后屈曲求解,riks方法通常不再适用,须引入惯性和黏滞阻尼力到动态或静态分析步以使求解稳定。
参考资料
知乎号-仿真设计;
正脉CAE博客;
江丙云等《ABAQUS工程实例详解》;
GB50017-2017《转自:标准》。