本文授权转载自公众号结构技术研究室

作者：蒋斌

01 剑胆琴心

薄壳于我，一直是一个令人神往的结构类别，可远观而不可亵玩。安东尼·高迪曾说过“直线属于人类，曲线属于上帝”，我觉得，曲面薄壳也是个神一样的存在。

也思考过像马德里赛马场、霍奇米洛克餐厅这样的经典薄壳之作为何诞生在计算软件和施工技术并不成熟的年代。也许手算年代的设计师理论功底更扎实、更有情怀、更纯粹，设计周期也更宽裕。

马德里赛马场  “混凝土诗人”爱德华多·托罗哈

霍奇米洛克餐厅  “薄壳大师”菲利克斯·坎德拉

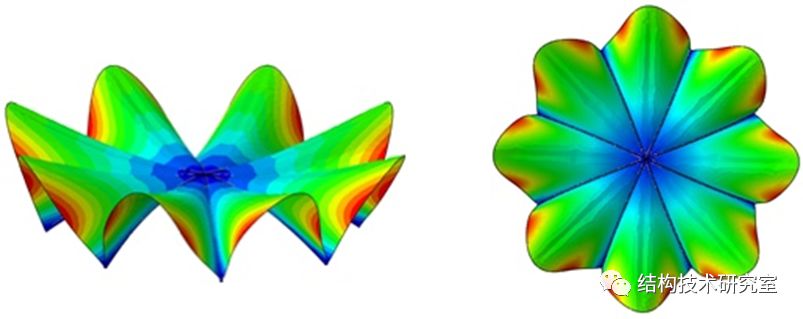
© 同济大学 任晓丹教授科研团队

02 项目一则

近期正好跟公司创作室合作一个项目，建筑局部有一处曲面造型，值得玩味。建筑师想做一个直立的“壳”，而由于受条件限制，壳的底部只能按铰接处理。概念上，底部铰接、顶部自由的墙体，难以成立；直觉上，似乎又成立。于是引发了后续的思考与实践。

罗马斗兽场

03 一张纸的承载力

作为双结构工程师的家庭，一直想找机会给熊孩子捋一捋她老父亲和老母亲的职业，消一消她脑海里我们头戴钢盔搬砖的刻板印象。于是出门前给她一张纸，出了一道题：

如何让一张纸能承托更多的重量？

谁说老鼠的孩子会打洞？答案在我意料之中…

接下来便是SOLO时刻。在我的引导下，一起用废纸做了四个简易模型。

工况1-矩形单层；工况2-柱面单层；工况3-柱面单层横行加肋；工况4-柱面双层（粘合）

加载过程充满欢呼声，一个比一个令人惊喜！

数字N表示加载至N+1本倒塌的前一级荷载

04 计算论证

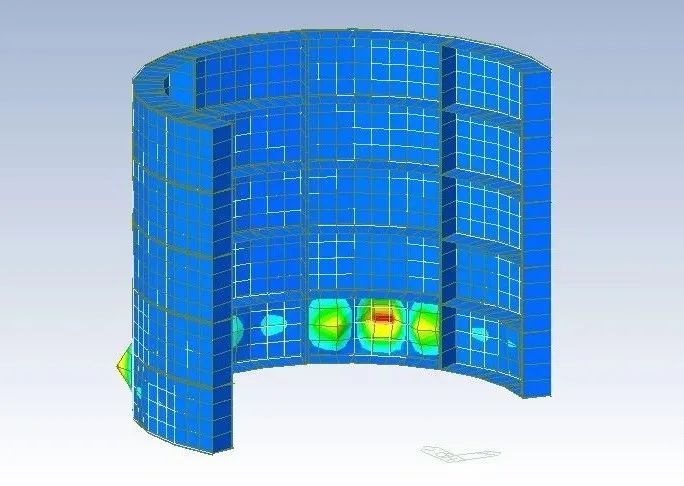
采用有限元软件建立四个工况对应的薄壳模型，进行屈曲分析。

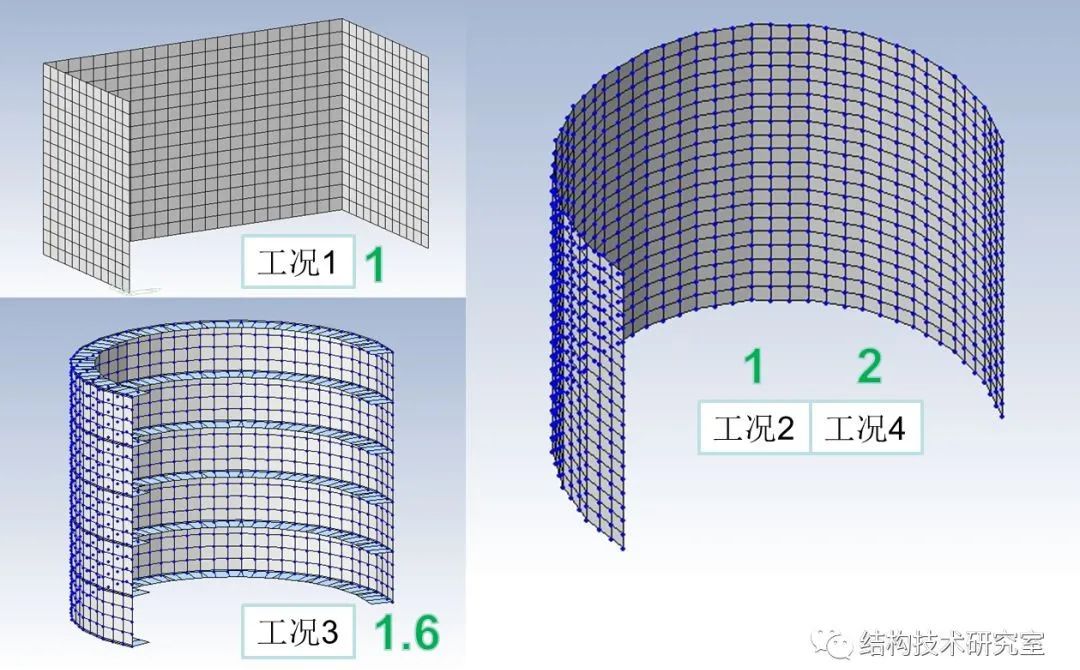
数字G为材料因子，即耗费的材料比例

以下为屈曲模态及稳定因子。

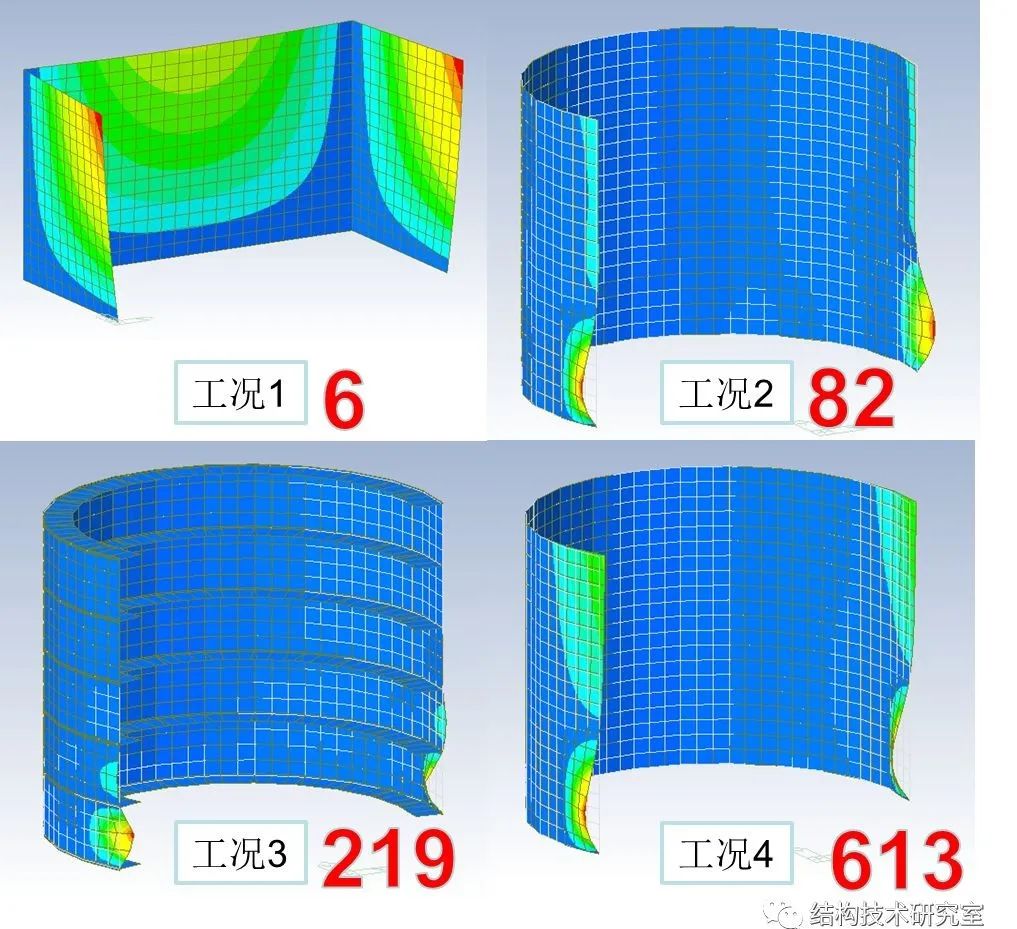
数字M为稳定因子，相当于结构承载能力的相对值

对比“试验”与数值计算结果，可以得出以下初步结论: 

（1）底部铰接、顶部自由的直立壳结构成立，至少能自成立；

（2）工况1～工况4加载试验与数值计算结果趋势基本一致，即承载能力呈递增趋势；

（3）该类壳的破坏均由失稳引起；

（4）增加厚度或面外肋板均能显著提高直立壳的承载力，从数值分析结果看，增加厚度更为有效；

（5）初始缺陷对稳定承载力有一定影响，工况3并未出现理想状态下的失稳模态，原因是肋板“焊接”中壳体的平滑度被破坏；

（6）实际项目中可根据承载力需求、建筑外观要求、材料用量（造价）角度综合选用合理的结构形式。

05 小结

通过实践与分析，让我对于直立壳有了更理性的判断依据，更有把握配合建筑师完成他的空间营造。

当然，也使小朋友对于结构工程师这个职业有了更进一步的认识：虽然平凡，但很科学，要努力学好各门基础学科。

从某个角度讲，我们是这样一群人：

用更少的材料创造出人类想要的空间

猜一猜，作为工况3的延伸

纵横向加肋后（G=1.8）

稳定因子M能达到多少？

给公众号留言数值即可