作者：童根树

浙江大学高性能建筑结构与材料研究所

为了理解双重抗侧力结构中的稳定计算，首先回顾钢结构稳定中几个重要的现象和结论。

1)两端简支压杆的临界荷载，由著名的欧拉公式计算：

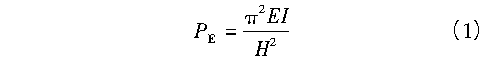
式中：EI是压杆截面的抗弯刚度；H是压杆长度。欧拉公式不仅提供截面抗弯刚度和构件长度与临界荷载的关系，进而提供压杆长细比的计算方法，而且对于设计人员来说，有非常重要的两点解读：截面的刚度决定了杆件的承载力；达到稳定极限状态时，截面仍然是完全弹性的(因为截面具有抗弯刚度EI)。即压杆达到了承载力的极限状态，但是截面没有达到极限状态。

2)图1所示的悬臂柱，其顶部与相邻的摇摆柱连接，则摇摆柱的临界荷载为：

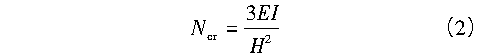
注意式(2)的重要意义：悬臂柱的刚度成就了摇摆柱的承载力。反过来说，要使摇摆柱具有承载力，则悬臂柱的截面必须具有刚度。

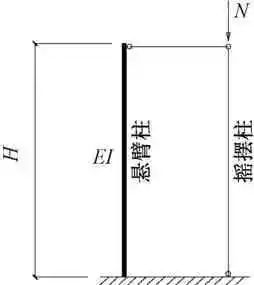
注：悬臂柱的刚度决定了摇摆柱的承载力。
图1 悬臂柱与摇摆柱的连接

通过上面两个简单的例子得到结论：不仅构件自身的刚度成就了自身的稳定承载力，相邻构件的刚度，也可以成为自身的承载力。

这样一来，当自身截面的强度足够，但自身刚度却不足以抵抗自身压力荷载时，相邻构件保有刚度就非常重要。

2.1 有摇摆柱的框架

设有摇摆柱的框架如图2所示，则框架柱的计算长度系数必须乘以放大系数η，η按式(3)计算：

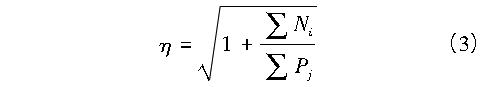
式中：∑Ni为所有摇摆柱上的轴力之和；∑Pj为框架柱上的轴力。采用放大了的计算长度，可以设计出比没有摇摆柱时更大的截面，从而保证有富余的刚度，为摇摆柱提供承载力。

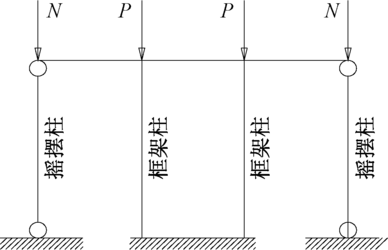
图2 设有摇摆柱的框架

2.2 防屈曲支撑

防屈曲支撑由直接受力的芯杆和不直接受力的外套钢管组成(图3)，两者之间填有混凝土，两者的界面上有环氧树脂层，使得力不会传递到外套管上。

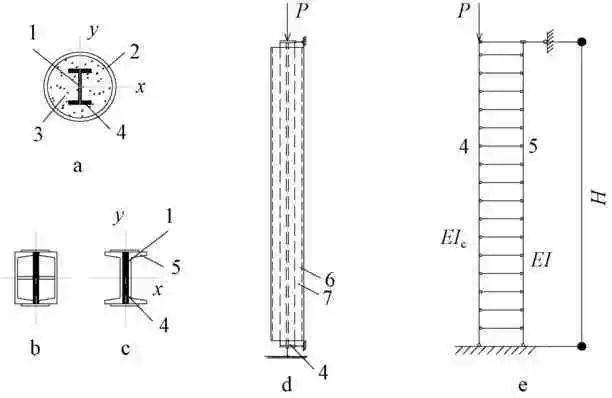
a—截面一；b—截面二；c—截面三；d—受力；e—分析模型。
1—环氧树脂；2—钢管；3—混凝土；4—被约束的压杆；

5—组合钢截面；6—外套管；7—芯杆。
图3 防屈曲支撑

防屈曲支撑的承载力为芯杆的屈服承载力。但这个承载力是由外套管提供的，外套管的刚度要求满足式(4)。

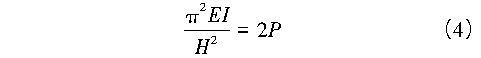
式中：系数取2是考虑了缺陷的影响。

即外套管的刚度为芯杆提供了承载力，芯杆本身可以不考虑长细比。

2.3 框架-支撑架结构

框架本身有侧移失稳的计算长度系数μsway>1，假设此时承载力是500 kN，但由于设计时希望框架采用μ=1，则承载力变为了800 kN, 这增加的承载力300 kN 是由支撑架的抗侧刚度提供的(图4)。因此必须采用某种设计方法，使得支撑架有这个富余的刚度。即支撑架本身按照普通的、常规的设计方法计算时，不能达到极限状态。

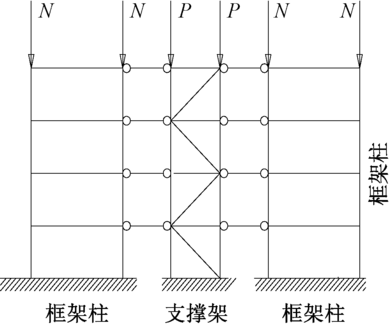
图4 框架-支撑架结构

这个富余的刚度即是GB 50017—2017的(8.3.1-6)式，即：

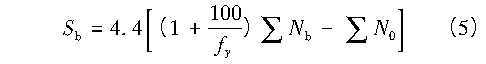
式中：∑Nb,∑N0分别为所有柱子无侧移失稳和有侧移失稳的弹塑性承载力，如果是摇摆柱，则有侧移失稳的承载力为0。

利用软件实现式(5)其实很不容易，JGJ 99—2015《高层民用建筑钢结构技术规程》对支撑架的构件(柱子和斜撑)采用应力比控制来实现，即：

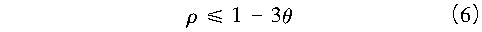
式中：θ为二阶效应系数。

摇摆柱框架、防屈曲支撑、框架-支撑架结构三者有共同的机理：

1)要确保起支撑作用的构件有富余的刚度以刚度换取被支撑构件的承载力。

2) 被支撑的构件与起支持作用的构件，存在某种形式的变形协调。即用框架柱的刚度，换取摇摆柱的承载力; 用支撑架的刚度，换取框架柱的承载力; 用外套管的刚度，换取芯管的承载力。

用相邻构件的刚度换取自身的抗压承载力，比直接采用增大自身截面来抵抗压力，有时候更加经济。在摇摆柱的情况下，增大自身截面没有意义。