来源：公众号“胡正宇结构视点” 作者：胡正宇

编者按：上周关于工字形截面钢悬臂梁的整体稳定承载力和计算长度系数探讨及中美加设计方法对比一文发布后，收到一些朋友的意见和反馈，现在此作稍作汇总，回复如下。

反馈意见1：

参考文献第一个名字错误，应该是转自：标准。

回答：

对，意见正确。现行中国钢规GB50017-2017已命名为“标准”(Standard)，不再是“规范”(Code)，谢谢指正。

反馈意见2：

是不是按17钢标附录C的表格来算悬臂梁的βb时，用不同的k值乘以L1去代替L1计算再去查表，即可得到不同支座约束条件下的βb系数？

回答：

如我文章中所说，17钢标附录C的悬臂梁βb表格是假定悬臂梁支座完全嵌固约束的，而且表中βb值的推导原理与美加规范有所不同。简单以kL1替代L1计算查表似乎不能得到不同支座约束条件下的βb系数，如果有这种情况且一定要按现行17钢标设计的话，最好的办法还是加强悬臂梁支座约束使其满足规范中规定的嵌固条件，对此可参考王立军大师的《悬臂梁的稳定》（王大师的原文链接）一文中推荐的构造要求去加强。如果既无法或无条件构造加强支座，那至少目前来说，只能按我文章中介绍的参考加钢标或美标公式(以kL代替L)去设计计算。

反馈意见3：

似乎有个问题，在应用举例中，悬臂吊车梁的支座约束是在上翼缘而非下翼缘，此情况不对应表中任何k。由于受压翼缘没有约束，k应该大于3.0.

回答：

应用举例中所给出的k=3.0是合适的。文中计算长度系数图表是来自CISC (Canadian Institution of Steel Costruction) 出版的《Roof Framing with Cantilever (Gerber) Girders & Open Web Steel Joists》，所列计算长度取值是根据Nethercot的论文以及由Ronald D. Ziemian主编的《Guide to Stability Design Criteria for Metal Structures》第5版中的图表稍作修改所得。原图表如下所示：

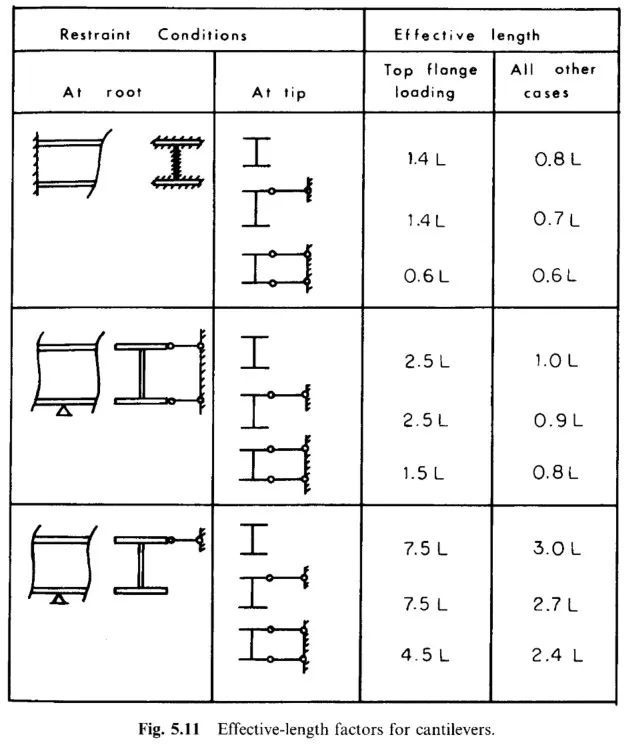
CISC那篇文章中的图表只是把金属结构指南一书中悬臂支座完全嵌固的情形删去，并将原图表支座处的梁的图示作了“形象化”处理，其目的是想使其显得更直观一些，但是现来这一改似乎反倒改出歧义来了。从以上原图中可以看出，对由backspan跨延伸出来的悬臂梁，当支座处上翼缘侧向约束，下翼缘简支无侧向约束且梁端集中力作用（非上翼缘）下，此时的k值应取3.0。需要注意的是，这种情形与我所举的悬臂吊车梁的例子的支座约束条件还是有一些细微的差别，那就是按上表中k=3.0模型，在支座处梁的腹板是受压的（因为简支作用在下翼缘），而我举的悬臂吊车梁的例子中支座处腹板上部受拉下部受压，因为支座是在上翼缘（如下图所示）。

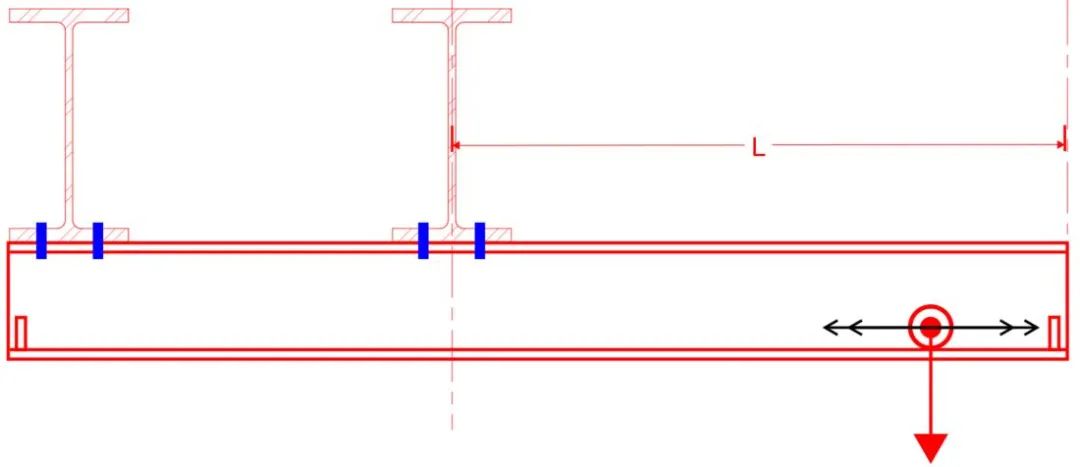
由于侧向无支撑薄壳在平面内受压时的稳定性最差，因此从理论上讲，悬臂吊车梁的整体稳定性要比上表中k=3.0模型的整体稳定性要稍好一些，至于好多少，Nethercot在他的另一篇文章The Effective Length of Cantilevers as Governed by Lateral Buckling中也有过研究，结论如下表绿色高亮文字所示：

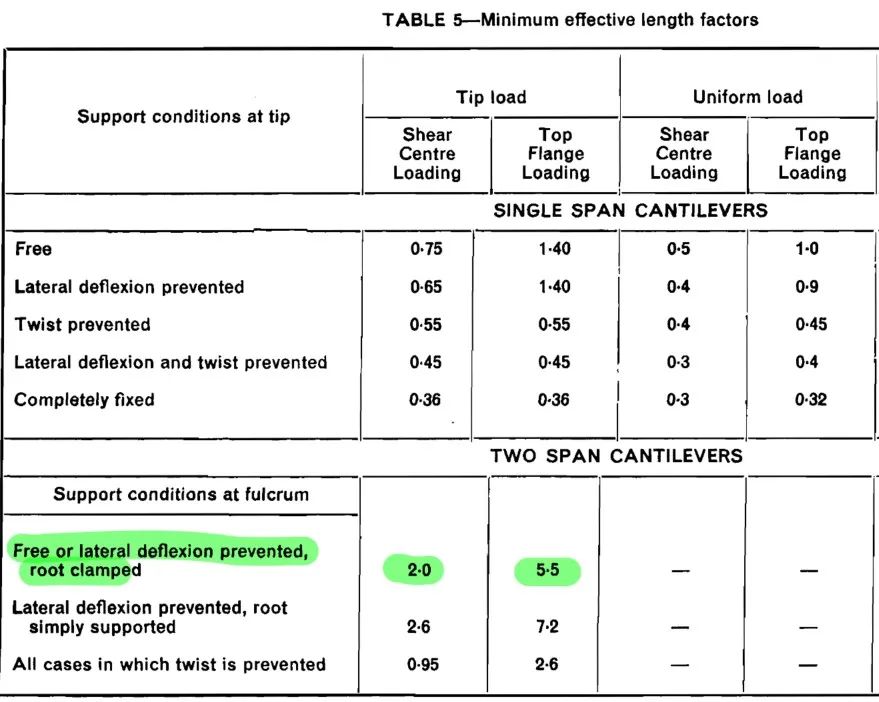
但是这种情形并没有被写进金属结构设计指南也没有被CISC的那篇文章采用，具体原因不详，但从逻辑上来讲，估计是由于论文图表中的计算长度系数是理论最小计算长度系数，而其clamped root悬臂梁的有效计算长度系数和支座处上翼缘侧向约束，下翼缘简支无侧向约束情况下的悬臂梁的有效计算长度系数相当（稍小），因此出于工程实践的保守考虑，仅考虑最不利情形的吧。总之，在工程实际中，如果遇到我举例中的悬臂吊车梁的情形，取其计算长度系数k=3用于设计校核梁的整体弯扭屈曲承载力应该是合适的。

反馈意见4：

那么问题来了，如果是楼面梁，有楼板，端部有封口铰接梁呢？

回答：

这个就比较好处理了，按中国规范条文 6.2.1：当铺板密铺在梁的受压翼缘上并与其牢固相连，能阻止梁受压翼缘的侧向位移时，可不计算梁的整体稳定性，只做强度验算即可；按美国规范其无支撑长度小于Lp，也是强度问题（没有弯扭屈曲的问题）；加拿大规范也是类似，在这种情形下即可定义为侧向有约束的情形，故只做截面强度验算，与计算长度系数无关。

反馈意见5：

最后举例中的一系列图标，为什么k值是一个范围，比如表中第一种情形，k=0.8~1.0，为什么？什么时候取0.8，什么时候取1.0? 原则是什么？

回答：

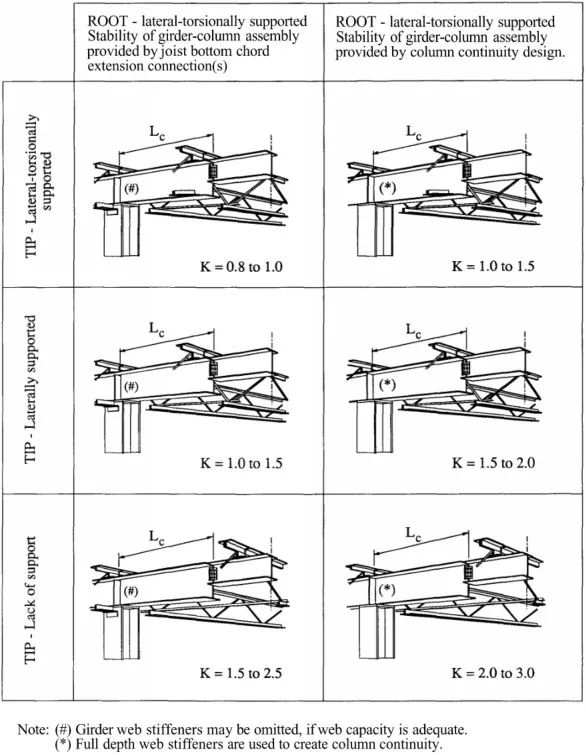
最后举例中的一系列图标同样是出自CISC (Canadian Institution of Steel Costruction) 出版的《Roof Framing with Cantilever (Gerber) Girders & Open Web Steel Joists》，其建议的计算长度系数是根据图示中给出的典型连接构造，考虑到由实际的OWSJ (Open Web Steel Joist)对梁的上下翼缘的侧向约束刚度往往并非如Nethercot表格中的计算模型那样在支座处或梁端理想化的侧向上翼缘或下翼缘水平约束，而对悬臂的计算长度系数在Nethercot 的计算长度系数的基础上做出适当调整后的结果，原则就是当支座侧向约束越刚（比如当悬臂支座的上下翼缘的侧向约束由与其正交的OWSJ的上下弦杆分别支撑，悬臂端的上下翼缘的侧向约束也由与其正交的OWSJ的上下弦杆提供时，当OWSJ的刚度越大，k值就可取越接近0.8，反之则宜取1.0。具体何为“越大”可由OWSJ的上下弦杆所能承受的轴向力来定量的衡量。但一般工程定性来说，悬臂较短，悬臂截面尺寸较小的悬臂梁，在这种情形下计算长度系数可取偏小（0.8），当悬臂较长且截面尺寸较大的悬臂梁，在这种情形下计算长度系数宜偏大取（1.0）。其余情形同理。

反馈意见6：

文章中提到Mcr是由一个参数Cb与一组与梁截面形状即侧向无支撑长度相关的数所得的乘积即可，类似中国规范中的βb*Wx，好像不太对？

回答：

Good Catch! 这是一个笔误，应该类似中国规范中的φb*Wx*f，即以弯矩形式表示的稳定抗弯承载力。

如有收获，分享转发 或 点亮“”▼