高层建筑结构的稳定性分析主要是控制结构在风荷载或水平地震作用下,重力荷载产生的二阶效应不致过大,不致引起结构的失稳、倒塌。

1.1 P-δ效应和P-Δ效应
结构的二阶效应是指轴向压力作用下在存在初始挠曲的构件上或竖向荷载作用下在存在侧移的结构上所产生的附加作用效应,属于结构分析设计中的几何非线性问题。二阶效应分为两种情况考虑:P-δ效应和P-Δ效应。
P-δ效应是指由于构件在轴向压力作用下,自身发生挠曲引起的附加效应,可称之为构件挠曲二阶效应,通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩,附加弯矩与构件的挠曲形态有关,一般中间大、两端小。P-Δ效应是指由于结构的水平变形而引起的重力附加效应,可称之为重力二阶效应,结构在水平力(风荷载或水平地震作用)作用下发生水平变形后,重力荷载因该水平变形而引起附加效应,如图1.1‑1所示,图中ui,wi和hi分别表示第i层侧向位移、重量和层高。
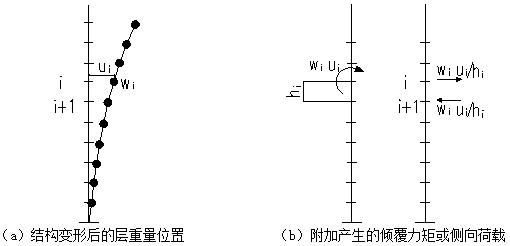
图1.1‑1由于层重量侧移产生的倾覆荷载
1.2 特征值屈曲分析方法
特征值屈曲分析用来预测一个理想线性结构的理论屈曲强度(分岔点)图1.2‑1所示。其优点是无需进行复杂的非线性分析即可获得结构的临界荷载和屈曲形状,并可为非线性稳定分析提供可参考的荷载系数。特征值屈曲分析中常用的求解方法有SubsPace法和BlockLanczos法。结构特征值屈曲的求解方程为:
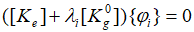 (1.2-1)
(1.2-1)
式中,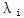 为第i阶屈曲特征值;[Ke]为结构的弹性刚度矩阵;
为第i阶屈曲特征值;[Ke]为结构的弹性刚度矩阵; 为结构的几何刚度矩阵;
为结构的几何刚度矩阵;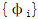 为第i阶特征向量,即该阶屈曲荷载作用时结构的变形形状,也即结构的屈曲模态。
为第i阶特征向量,即该阶屈曲荷载作用时结构的变形形状,也即结构的屈曲模态。
特征值屈曲分析方法相当于教科书里的弹性屈曲分析方法。例如,一个柱体结构的特征值屈曲分析的结果,将与经典欧拉解相当。但是,初始缺陷和非线性使得很多实际结构都不是在其理论弹性屈曲强度处发生屈曲。因此,特征值屈曲分析经常得出非保守结果,通常不能用于实际的工程分析。但特征值屈曲分析可以为结构提供失稳的上限荷载参考值和一致缺陷分析所需要的屈曲模态。此外,特征值屈曲分析结果还可以帮助工程师从多种荷载组合中迅速找出最不利荷载组合,从而确定非线性分析的目标工况。
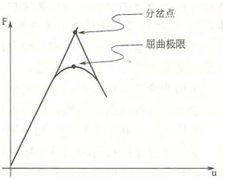
图1.2‑1 分岔点示意图
1.3 刚重比计算方法
如图1.3‑1(a)所示的竖直悬臂杆顶端作用有集中轴向力P,分布的水平力使悬臂杆产生了水平变形,由集中轴向力P引起的P-Δ效应对水平力作用下悬臂杆的位移和内力的放大系数F可表示为:
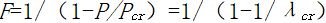 (1.3-1)
(1.3-1)
式中: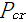 为悬臂杆的屈曲荷载;
为悬臂杆的屈曲荷载;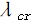 为悬臂杆的屈曲因子,
为悬臂杆的屈曲因子,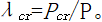 。
。
假如竖直悬臂杆代表一栋高层建筑结构,分布轴向力代表重力荷载,分布水平力代表风荷载或地震作用,如图1.3‑1(b)所示。重力荷载产生的P-Δ效应对风荷载或地震作用下的位移和内力的放大系数可表示为:
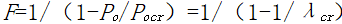 (1.3-2)
(1.3-2)
式中: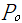 ,
,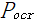 和
和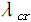 分别为该高层建筑结构的总的重力荷载、屈曲荷载和屈曲因子,
分别为该高层建筑结构的总的重力荷载、屈曲荷载和屈曲因子,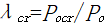 。
。
由式(1.3-1)可知,高层建筑结构P-Δ效应的大小可通过屈曲因子 的大小来判别。若控制P-Δ效应小于或等于10%(即F≤1.1),则相当于控制屈曲因子
的大小来判别。若控制P-Δ效应小于或等于10%(即F≤1.1),则相当于控制屈曲因子 大于或等于10。
大于或等于10。
(a)集中力轴向力 (b)分布力轴向力
图1.3‑1 承受水平力及轴向力的悬臂杆
张小勇,周立浪,扶长生(文献[高层建筑结构基于整体稳定的周期上限研究])提出等截面均质悬臂杆的屈曲临界荷载和屈曲因子分别为公式:
屈曲临界荷载 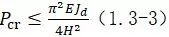
屈曲因子 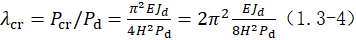
式中H为房屋高度;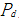 为顶部作用竖向集中力;
为顶部作用竖向集中力;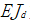 为截面侧向刚度。
为截面侧向刚度。
《高层建筑混凝土结构技术规程》(JGJ3-2010)以结构按弹性分析的P-Δ效应对结构的内力和位移增量控制在某一区间,提出了整体稳定控制和计算分析的要求。当按弹性分析的P-Δ效应小于或等于5%时,计算分析中可不考虑其的影响; 当按弹性分析的P-Δ效应大于5%而小于或等于10% 时,计算分析中需要考虑其的影响;当按弹性分析的P-Δ效应大于10% 时,重力荷载产生的P-Δ效应将过大,以致引起结构的整体失稳倒塌,这种情况是不允许的。
对于剪力墙结构、框架剪力墙结构和筒体结构,规程JGJ 3—2002和规程JGJ 3—2010与规定JZ102—79和规程 JGJ 3—91一样,同样采用等效刚度和等效荷载的概念,在假定各楼层的重力荷载基本上沿建筑高度均匀分布的条件下,提出了等效刚重比rsw的计算公式:
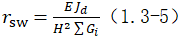
式中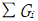 为总的重力荷载设计值。
为总的重力荷载设计值。
当各楼层的重力荷载基本上沿建筑结构高度均匀分布时,顶部作用的等效集中重力荷载可用总的重力荷载表示为:
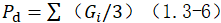
将式(1.3-6)代入式(1.3-4),可得:
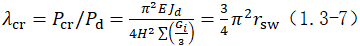
从式(1.3-7)可知,控制刚重比大于或等于1.4,相当于控制结构的屈曲因子大于或等于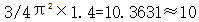 。
。
随着高层建筑结构高度的不断增加和体形的日益复杂化,由于采用了等效刚度和等效荷载的概念,等效刚重比公式(1.3-5) 在应用到实际结构设计中面临一些问题。例如上海中心、平安中心和中南中心等超高层项目,由于其塔楼体形下大上小的特性,大部份质量分布在下部楼层,而等效刚重比公式(1.3-7)按塔楼质量均匀分布的假定导出,因此上述项目在验算结构的整体稳定性时均考虑了体形特性,对塔楼质量均匀分布的假定进行了修正。
综上所述,高层建筑结构的整体稳定性控制和验算可以通过结构的屈曲因子大小来判别。规程DBJ 15-92—2013第5.4.5条规定:高层建筑结构的整体稳定性也可通过有限元特征值法进行计算。由特征值算得的屈曲因子不宜小于10。当屈曲因子小于20时,结构的内力和位移计算应考虑P-Δ效应的影响。
1.4 等效计算长度
实际工程中遇到跨层柱、巨柱等需要在弹性约束条件下准确计算柱的等效计算长度。在整体有侧移模型中,在欲求计算长度的柱上加垂直于柱横截面的单位力,通过计算分析模型的第一阶屈曲模态和对应的临界荷载,最后由欧拉公式可反算出杆的等效计算长度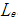 。
。
屈曲临界荷载 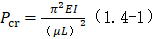
等效计算长度 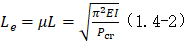
式中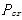 为临阶荷载;E为材料弹性模量;
为临阶荷载;E为材料弹性模量;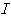 为截面惯性矩;
为截面惯性矩;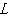 为杆的实际长度。
为杆的实际长度。

(1)不输出屈曲因子
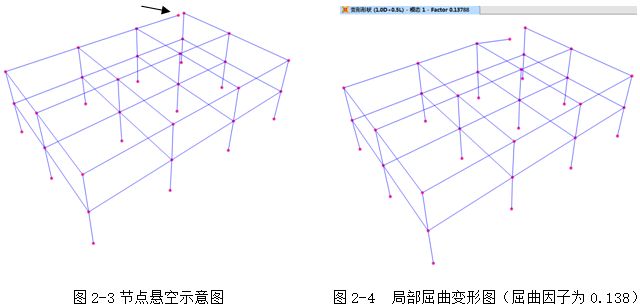
屈曲分析计算后,软件没有输出屈曲因子,常见原因是结构构件节点出现悬空或者存在虚梁等情况。
如图2 -1所示,由于左上角的构件悬空,导致结构的计算时间明显加长,计算耗时为20分钟,并且没有输出屈曲因子结果。需要把悬空构件进行连接处理,构件连接后(图2-2),计算时间仅需30s,结构整体的屈曲因子为25.470。
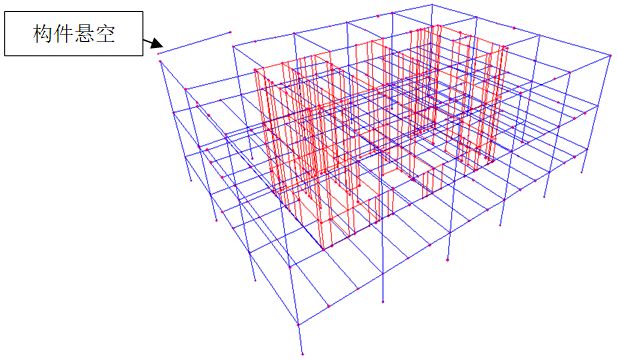
图2‑1构件悬空

图2‑2屈曲变形图(屈曲因子为25.470)
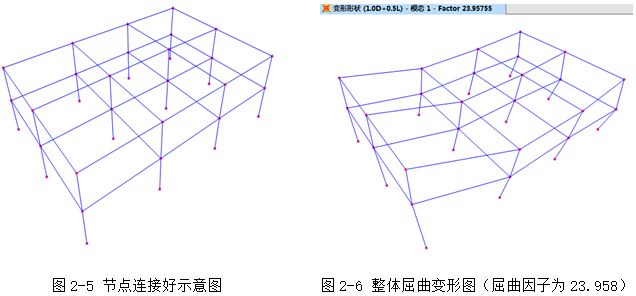
(2)输出的屈曲因子很小
当出现屈曲因子很小时,可通过查看屈曲模态,可能是个别构件没有搭接好或者构件刚度不够引起。
如图2-3所示,由于右上角的节点没有连接好,导致结构产生局部屈曲,屈曲因子只有0.138(图2-4),需要把没有连接好的节点进行连接处理,节点连接合理后(图2-5),结构整体的屈曲因子为23.958(图2-6)。

广州良业大厦塔楼3建筑面积5.2万平方米,地上33层,建筑高度149.55m,见图3-1和图3-2。抗震设防烈度为7度,设计地震分组为第一组,场地类别为II类,基本风压为0.5kN/m2,地面粗糙度为C类,体形系数依据风洞试验。
塔楼3结构平面形状为三角形平面,但把平面的三个角切除,减小结构的扭转效应,改善空间受力性能。外框柱1-16层采用圆形混凝土内置型钢柱,(含钢率4%~6%);外框梁采用混凝土梁,截面为500mm×800mm和400mm×800mm,框架梁截面为500mm×800mm和600mm×900mm。主要竖向构件尺寸见表3-1所示。
(1)整体稳定性分析
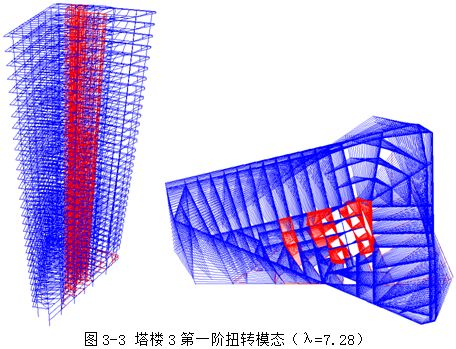
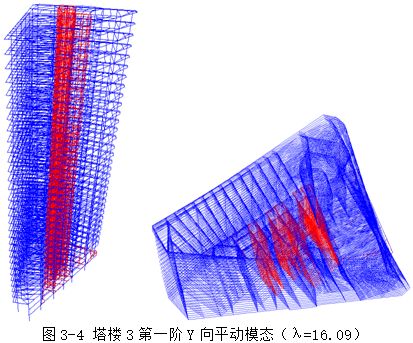
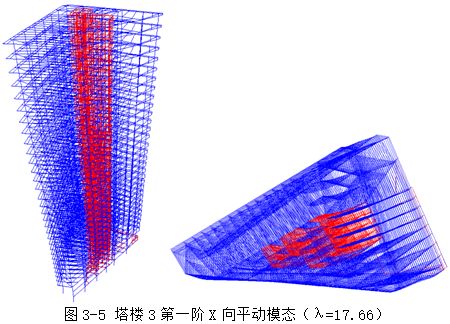
图3-3,图3-4,图3-5分别为塔楼3第一阶扭转模态、第一阶Y向平动模态和第一阶X向平动模态,其中第一平动屈曲模态特征值λ=16.09>10.0,满足规范要求。
(2)构件稳定性分析
塔楼3的外框柱在1~3层均存在跨层的情况,缺少楼层内梁板的侧向支撑,有必要对跨层外框柱的实际计算长度进行分析。
通过跨层柱的两端加轴线方向上的力,进行屈曲分析后得到柱的屈曲模态以及屈曲荷载系数,即可求得柱的屈曲临界荷载。然后按照欧拉公式 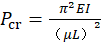 ,反算出柱的计算长度
,反算出柱的计算长度 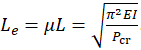 。
。
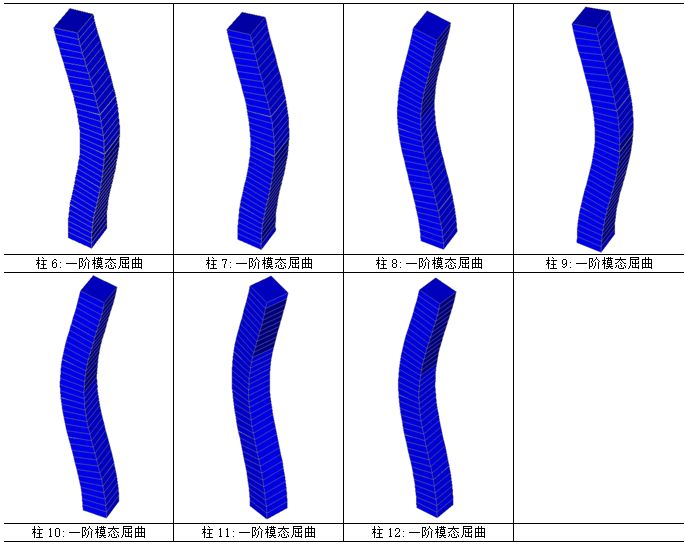
按照前述方法,对跨层构件进行屈曲分析,各构件编号图和柱的屈曲模态如图3-6和表3-2所示。
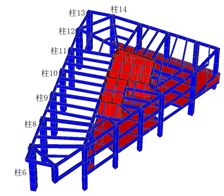
图3-6 1-3层(塔楼3)构件位置图
表3-2 跨层柱的模态屈曲形状
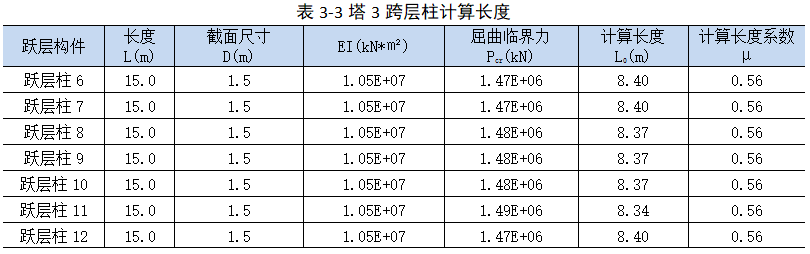
将计算所得的计算长度系数和柱参数列于表3-3表。由表3-3结果显示,跨层柱的计算长度系数小于1.0,在整体模型计算中,跨层柱的计算长度系数偏于保守,仍按1.25输入。

来源:微信公众号“广东省院结构安全顾问”