在上一期“说桥”（上期文章▶：重力刚度的本质）中，比较通俗地解释了“重力刚度”的意义，并称其为几何刚度的一种。

文章推出后，引起了许多同仁的兴趣，所以本期拟继续讨论一下这个问题。

从几何非线性理论角度理解

为了阅读方便，把前文的式（3）在这里重复给出：

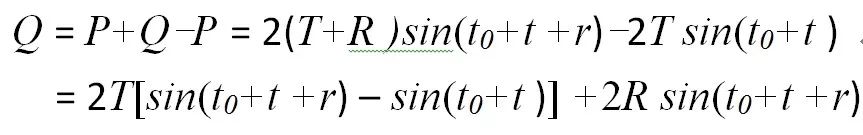     (3)

为了分析结构刚度，可将Q看作竖向外力P的增量ΔP，r则为对应的角位移增量Δt（也是反映竖向变形的变量），R为对应的内力增量ΔT。为简便，设：g₁=sin(t₀+t)，g₂=sin(t₀+t+Δt)，g₁₂=g₂–g₁。g₁和g₂是反映索在不同受力状态下几何构形的函数，因此g₁₂反映的是由于ΔP的作用使索几何构形发生的变化量的函数，且当不考虑几何非线性影响时，该值为零。注意到g₂=g₁₂+g₁，则式（3）可改写为如下增量形式：

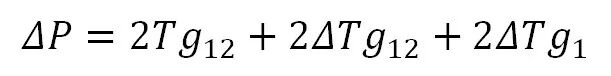   (5)

把方程两边同除以角位移增量Δt，便得到割线刚度表达式如下：

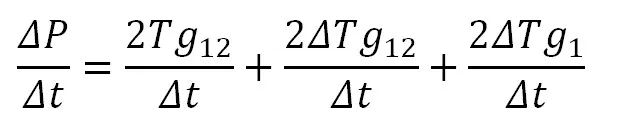    (6)

大家知道，增量形式的割线刚度是指力-位移关系曲线上两个点之间连线的斜率，因此式（6）是索从承受外力P状态变化到承受外力P+ΔP状态这个增量区间的割线刚度（见图5）。式（6）右端第一项是几何构形改变与原有内力T（P的作用效应）相互作用产生的竖向刚度，也就是几何非线性理论中的几何刚度（见“李乔说桥-12 再谈桥梁几何非线性”）；式（6）右端第二项是几何构形改变与新增内力ΔT相互作用产生的竖向刚度，即几何非线性理论中的大位移刚度。而式（6）右端第三项则是原有几何构形与新增内力ΔT相互作用产生的竖向刚度，即线性刚度。

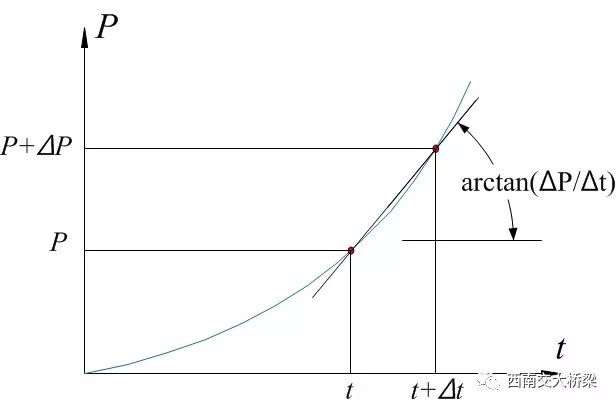
图5 割线刚度

从前一期文中的图3可以看出，索的初始构形为一折线形（图中黑线），相当于由两根杆件组成的桁架，因此具有初始的线性刚度。而如果t₀=0，则表示索的初始构形为一连接A和B的水平直线（图6黑线所示），前一期文中的公式(4)*是t₀=0情况索的切线刚度表达式。从概念上和公式（4）都可以看出，当无外力P时，竖向切线刚度为零。而只要有横向外力P，就会引起角度t，使原来的水平索变成一个桁架，因而考虑非线性效应时就有了竖向刚度。

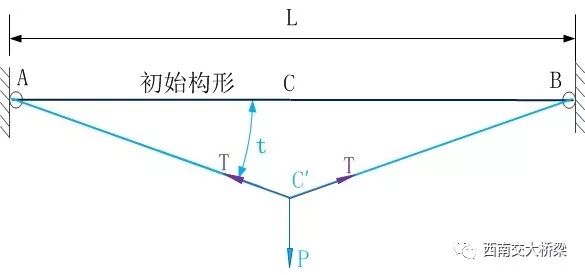
图6 初始构形为水平直线的索

t₀不等于0情况的切线刚度为如下形式：

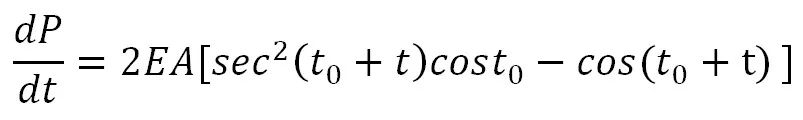         (7)

由于式（7）中考虑了初始的角度t₀，因此该式所表示的切线刚度包括初始构形（图3中的桁架ACB）的线性刚度。

以上分析为了简单，将外力Q与P都作用在同一个点C处。若二者不在同一点，例如Q作用在AC之间，则也有类似的特性，只不过此时Q方向的刚度表达式更复杂一些，并且几何构形的变化也不能简单地用t和r表示，外力-位移曲线也与图5有所差别。

一般桥梁结构的重力刚度

从上面的分析可以看出，重力刚度只是悬索结构几何刚度的一种，是由恒载重力产生的几何刚度。假如把凡是恒载重力产生的几何刚度都叫作重力刚度，那么除了悬索桥结构以外，其他桥型结构有没有重力刚度？

答案是肯定的。在考虑几何非线性效应时，其他桥型结构因存在几何刚度和恒载重力，因此当然也存在重力刚度。但从几何刚度的表达式可以看出，几何刚度的数值大小及正负（并不一定都是正值）取决于基准状态的内力和几何构形的改变量。在悬索桥以外的其他桥型结构中，由于主要承重结构不是柔性的悬索，重力刚度远比悬索桥结构小，而且很多时候还是负的，即重力刚度起负作用。典型的例子是受压的桥墩柱子，上部结构及自身的重力越大，因非线性侧弯变形引起的附加弯矩就越大，竖向刚度就越小（类似压杆稳定问题）。

对于斜拉桥结构，虽然作为主要承重结构的斜拉索也是柔性索，但从前面的分析可知，重力刚度是指索的两个支点之间的各点抵抗竖向变形的能力，索本身的重量和加劲梁的重量也是作用在支点之间的，而斜拉索利用的是两支点连线方向的刚度，索的自重使这个连线刚度降低，梁的自重作用在索端部，因此在斜拉桥中不能利用重力刚度来抵抗活载变形。

（*注：更正：式（4）中括号内第二项原误为+cos²t，应为–cost）

来源：公众号“西南交大桥梁”

 李乔教授原创文章，仅代表作者本人观点，仅供参考，不妥之处，敬请指正