“转自:“
来源:知乎“猪小宝”
先看一个最近比较火的建筑抗震课的视频,理解一下地震的本质。文末有《地震力到底是怎么算出来的》,系列文章汇总。
在这个问题之前,我想先问一句,「如果不是央视新楼,而是一栋普普通通的建筑物,您知道它在地震作用下会如何变形吗?」

建筑物在地震下的变形,简单说,取决于两方面。类似的,你被别人揍了,你的受伤程度也取决于两方面:你是不是施瓦辛格,对方是不是施瓦辛格。同样,建筑物的地震响应,也取决于内外两方面:建筑物自身的特性、地震的特性。同样的地震,不同的结构,变形就不同;同样的结构,不同的地震,变形也不同。
下面的内容更侧重于建筑物在地震作用下如何变形,而央视新楼只是其中一个特殊的例子。如果您不知道普通建筑物在地震作用下如何变形,不知道周期、振型、阻尼的意思,让我们一块儿从高中物理开始吧。
首先看看我们身边的例子,刚刚好,身边就有一个例子。胖馃同志贡献出她们的猫爬架作为结构动力学入门的第一课。
看,猫爬架上有两个球,一个拴在绳子上,一个绑在竖直放置的弹簧上,它们都可以来回摆动,充当猫猫们的假想敌。
我们先看用绳子挂着的这个球,近似的,我们可以把它看成一个理想的单摆。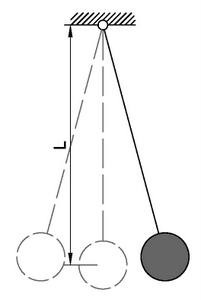
我们知道,或者说,伽利略在1583年就已经知道,单摆的摆动周期不变,虽然每次摆动的幅度变小,但是每次摆动所花的时间不变。我们以前的那种大摆钟,用的就是这个原理。单摆摆动的圆频率,等于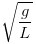 ,g 是重力加速度,L 是摆的长度。或者,如果您不习惯圆频率,我们可以用周期来表示,单摆摆动的周期是
,g 是重力加速度,L 是摆的长度。或者,如果您不习惯圆频率,我们可以用周期来表示,单摆摆动的周期是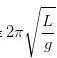 ,L 的单位是长度,g 的单位是长度除以时间的平方,带进去,得出的周期的单位就是时间。
,L 的单位是长度,g 的单位是长度除以时间的平方,带进去,得出的周期的单位就是时间。
同样的道理,我们再看一下弹簧顶着的球,它来回摆动的周期是多少呢?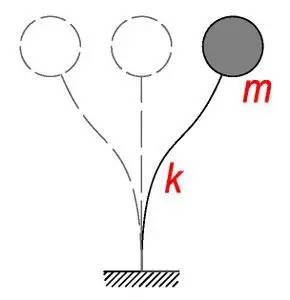
弹簧顶个球,来回摆动的周期取决于两个参数,球的质量 m 和弹簧的侧向刚度 k,摆动的周期是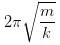 。k 的含义是使小球发生单位位移的力,也就是说,我作用 k 的力在小球上,小球就位移 1,我作用 3k 的力,小球就位移 3。m 的单位是力除以重力加速度,k 的单位是力除以长度,m 除以 k 的单位就是长度除以重力加速度,也就相当于
。k 的含义是使小球发生单位位移的力,也就是说,我作用 k 的力在小球上,小球就位移 1,我作用 3k 的力,小球就位移 3。m 的单位是力除以重力加速度,k 的单位是力除以长度,m 除以 k 的单位就是长度除以重力加速度,也就相当于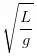 。或者,我们用圆频率来表示,它的自振频率是
。或者,我们用圆频率来表示,它的自振频率是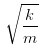 。
。
这位看官不耐烦了,我们在讨论建筑抗震呢,你扯什么弹簧小球?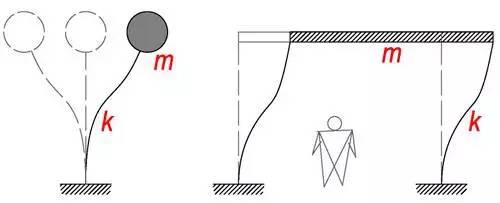
别着急,上面这张图能不能回答您这个疑问呢?左边是弹簧顶个球,右边是一个简化的一层的小房子。您说,它们在某种程度上是不是一样的呢?
对于右边的建筑结构模型来说,m 是整层的质量,k 是整层的柱子侧向刚度之和。小房子来回摆动的特性,跟左边的弹簧小球是完全等价的。对于一层的房子,我们可以称之为「棒棒糖」模型。
那如果是两层、三层、八十层的房子呢?很简单,一层的是「棒棒糖」模型,多层的就是「糖葫芦」模型。比如底下这个五层的房子,就是一个有五个山楂的糖葫芦串。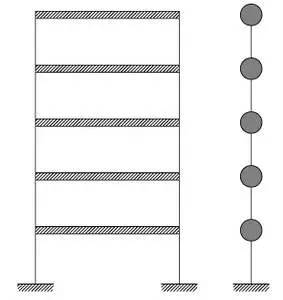
问题又来了,对于一层的「棒棒糖」,振动频率是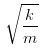 。那对于多层的「糖葫芦」,振动频率是多少呢?
。那对于多层的「糖葫芦」,振动频率是多少呢?
对于一层的「棒棒糖」,质量 m 和刚度 k 都是一个数值,对应的振动频率也是一个数值。而对于多层的「糖葫芦」,质量和刚度都变成了矩阵,对应的频率也变成了好几个。计算原理一样,只是都变成了矩阵层面的。我们从最简单的两个山楂的「糖葫芦」开始。
这时候,m 变成了矩阵 M,k 变成了矩阵 K,频率是两个矩阵特征值的开平方,一共两个: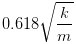 和
和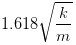 ,两个频率对应的特征向量分别是ø1和ø2。
,两个频率对应的特征向量分别是ø1和ø2。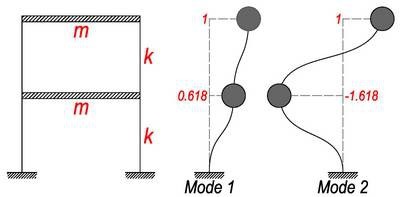
什么意思呢?意思就是这个二层房子有两种振动模式。第一种是图中的 Mode1,一起向同一个方向振动,振幅之比是 1 比 0.618,频率是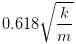 ;第二种是图中的 Mode2,两个小球振动的方向相反,振幅之比是 1 比 -1.618,频率是
;第二种是图中的 Mode2,两个小球振动的方向相反,振幅之比是 1 比 -1.618,频率是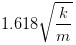 。
。
我们所说的结构本身的振动特性,指的就是这个东西。结构的质量分布、刚度分布对结构自振特性的影响。看上去类似的房子,因为质量、刚度的差异,很可能有着截然不同的自振特性。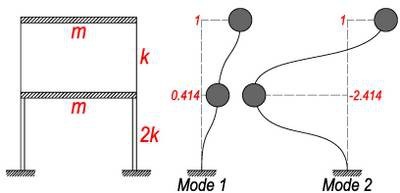
比如,如果我们让一层的柱子更粗壮一些,一层的刚度变为 2k,其余不变。它的振型就变成了上面这样。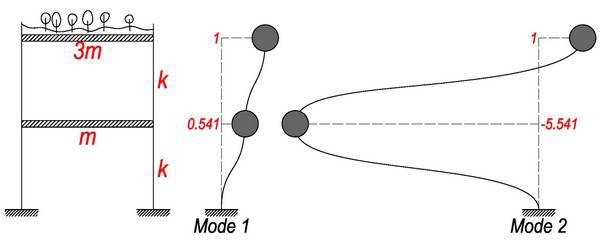
再比如,我搞一个屋顶花园,花草树木加上种植土,让屋顶的质量变成了 3m,其余不变。这个房子的振型又变样了。即使不用我说,相信您也能直观的感受到它对自振特性的影响。
那位看官又说了,振型有什么用啊?某种意义上,我们可以用振型来表示一切可能的振动模式。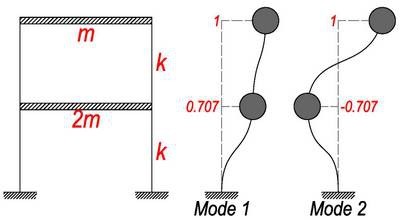
比如这个两层小房子,很普通,也很有代表性。柱子一样粗,都是k,屋顶轻一些,因为上面什么都没有,二层楼板重一些,因为上面放着家具什么的。它的两个振型是上图这样的。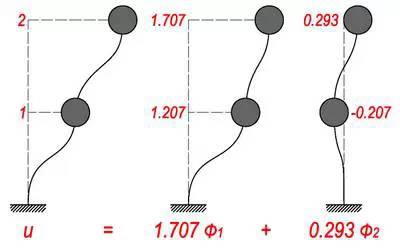
比如,如果我们想得到某种振动模式,使得一层的振幅为 1,二层的振幅为 2。我把 Mode1 乘以1.707倍,1乘1.707等于1.707,0.707乘1.707等于1.207;再把 Mode2 乘以0.293倍,1乘以0.293等于0.293,-0.707乘0.293等于-0.207。然后把这两个加起来,1.707加0.293就等于2,1.207加-0.207等于1。换言之,我想要的二层与一层振幅之比为2的振动,其实就等于1.707倍的第一振型和0.293倍的第二振型的叠加。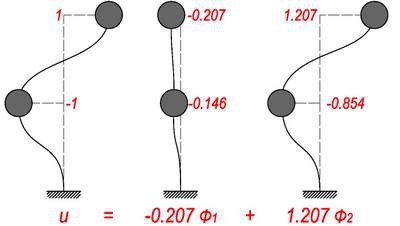
再比如,一个二层振幅为 1,一层振幅为 -1 的振动模式,可以用-0.207倍的第一振型再加上1.207倍的第二振型来表示。说白了,这是一个二元一次方程组,你可以线性组合出你想要的任何振动模式。
如果是我们上面举的那个五层楼的例子,因为它有五个山楂,所以它有五种振型,也就是五种振动模式。下图摘自乔普拉《结构动力学》第12章,就是这个质量、刚度均匀分布的五层楼的五个振型: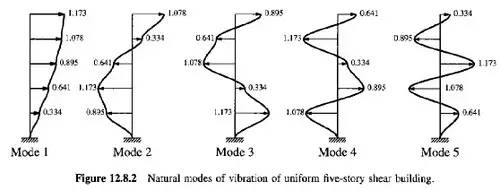
请注意,我们以上的讨论,都是在理想化的二维空间内。现实中没有二维建筑,所以实际的问题比这要复杂的多。实际的建筑结构,可以南北方向振动,也可以东西方向振动,还可以绕着自己的中心旋转,所以一个实际的二层房子,至少有6个振型。如果考虑到竖向地震的作用,那结构不光可以x向平动、y向平动、z向旋转,还可以z向平动、x向旋转、y向旋转,一切都变得无比的复杂。但复杂归复杂,其中的道理是类似的,只是拓展到了三维空间而已。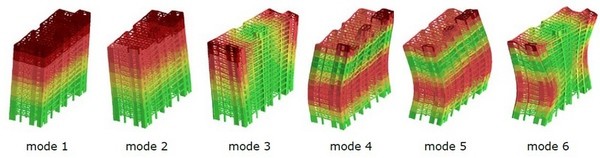 举一个小例子,上面就是我做过的一个实际设计的前六个振型。第一振型是长边方向平动,第二振型是短边方向平动,第三振型是扭转。
举一个小例子,上面就是我做过的一个实际设计的前六个振型。第一振型是长边方向平动,第二振型是短边方向平动,第三振型是扭转。
我知道,从上面的两个小球的振型,直接跳跃到这个实际三维建筑物的振型,跨越实在是有点大。但我觉得,如果你明白了两个小球的振型,至少你可以明白这些花花绿绿的振型图是在说什么。
以上的部分讨论的是结构自身的自振特性,下面我们进入结构在外力作用下的变形问题。
我们不是结构动力学的专业课,所以呢,简便起见,我们只讨论一层的「棒棒糖」模型。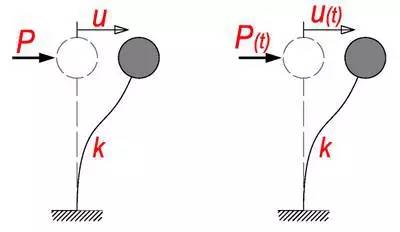
如果我施加一个大小为 P 的力给小球,小球发生的位移为 u,根据刚度 k 的定义,k 是单位位移对应的力,所以我们可以知道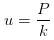 。但是,如果P不是定值,而是一个随时间变化的函数呢?此时,位移 u 肯定也是一个随时间变化的函数。它们之间的关系如何呢?是简单的
。但是,如果P不是定值,而是一个随时间变化的函数呢?此时,位移 u 肯定也是一个随时间变化的函数。它们之间的关系如何呢?是简单的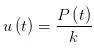 么?
么?
可能直觉告诉你,肯定不是。事实上也确实不是。为了弄清 u(t) 和 P(t) 之间的关系,我们先从自由振动说起。什么是自由振动呢?就是假设我施加的 P 是瞬间完成、瞬间释放的,或者说,我用手把小球拽开,然后突然放手,之后再也不施加任何外力。在这种情况下,小球的振动是什么样子的呢?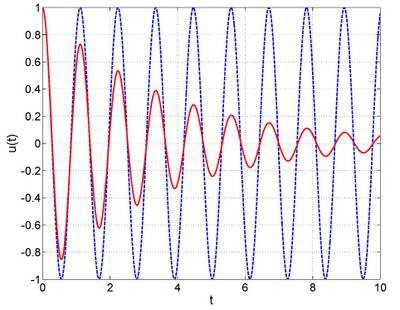
理想状态下,小球的位移-时间曲线是图中的这条蓝色虚线,我相信这条曲线的含义是高中物理的内容。当时间为 0 的时候,位移是 1,也就是我用手把小球拽到 1 的位置,然后放手。之后小球就一直来回摆动,并且直到永远,除非有其它外力再作用到小球上。小球每次的振幅都相同,振动的圆频率是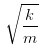 。
。
但我们知道,现实世界里没有一直摆动的小球,就像没有绝对光滑的平面、没有绝对笔直的直线。所以呢,常识告诉我们,小球不会一直摆动,它摆动的幅度会越来越小,慢慢就摆不动了。我们把这种效应称做阻尼。因为阻尼的存在,所以小球不会一直摆动下去。对于一般的建筑结构,阻尼比大约为 0.05,考虑 0.05 的阻尼比之后,小球的位移曲线是图中的红色实线。跟蓝色虚线相比,红色实线的频率略小一点点,也就是周期略长一点点。
如果我们的P(t)是一个正弦函数呢?也就是 P 等于某个常数乘以 sin(wt)。我们已经知道,我们的「棒棒糖」体系的自振频率是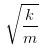 ,我们把它称之为 wn。我们施加的这个呈正弦函数变化的力,也有一个变化的频率,也就是 w。就像我们之前所说的,wn 是结构自身的特性,w 是外力的特性。结构的变形响应取决于这两者之间的相对关系。
,我们把它称之为 wn。我们施加的这个呈正弦函数变化的力,也有一个变化的频率,也就是 w。就像我们之前所说的,wn 是结构自身的特性,w 是外力的特性。结构的变形响应取决于这两者之间的相对关系。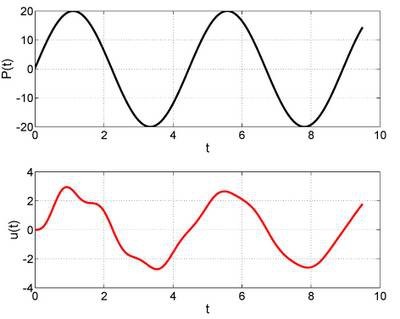
如果外力 P 的变化频率 w 是结构自有频率 wn 的 0.25 倍,也就是说,图中的黑色曲线代表的外力的变化频率是上面自由振动的图中蓝色虚线的频率的四分之一。或者,黑色曲线的周期是4秒多,自由振动的蓝色虚线的周期是1秒左右,外力的周期是结构自由周期的 4 倍。这时候,小球在这个外力作用下的变形是图中这个红色曲线,最大位移在 3 左右。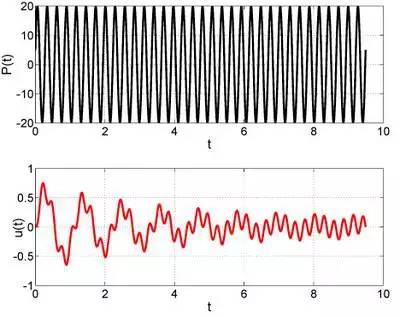
如果外力P的变化频率是结构自有频率的四倍,或者说,外力的变化周期是结构自由振动的周期的四分之一,此时结构的位移响应是上面这样的,最大位移 0.8 左右。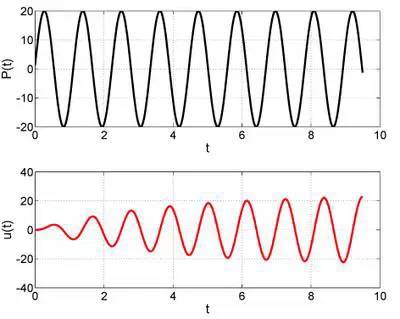
如果外力的频率就等于结构本身的频率呢?这时候,小球的位移越来越大,前 10 秒之内,最大值已经突破了 20,远远大于上面的 3 或者 0.8。
为什么呢?为什么外力的频率和结构本身的自有频率相等的时候,位移会如此之大呢?聪明的看官可能已经明白了,这就是所谓的「共振」。我们小时候听说的故事,过去欧洲某只部队齐步走过桥,结果齐步走的频率跟桥的自振频率一样,于是,桥就塌了。
即使不是正弦函数的外力,其它周期函数的外力同样也会造成「共振」。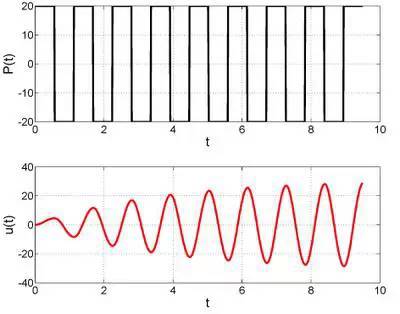
比如,我施加一个周期性的矩形外力,其频率等于小球的自振频率,同样,我们可以看到小球的位移幅度非常之大。
那位看官说了,为什么要说这些呢?这些跟地震有什么关系?因为地震同样也可以看作是一种输入的外力,同样也有自己的频率,同样也会存在这种「共振」。我们知道,结构的自振频率近似跟高度相关。比如很多地震,低层建筑破坏严重,而高层建筑破坏很小,因为大多数地震的频率跟低层建筑的频率相近。还有一些地震,比如墨西哥城地震,低层建筑几乎没有破坏,而高层建筑破坏非常严重,这就是因为墨西哥城地震的频率跟高层建筑的频率非常相近。
再回到我们的单小球「棒棒糖」模型,我们已经让它经受了自由振动、正弦函数外力、周期矩形外力。但是呢,这些都是非常理想化的状态,现实中不会有完美的正弦函数外力。
下面,我们就来真格了,让我们的「棒棒糖」模型经受真正的地震考验。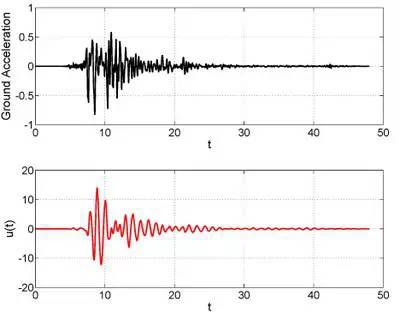
如果1995年阪神地震的时候,我们的这个单小球「棒棒糖」模型刚好就在神户。地震输入的外力是上面的黑色曲线,单位是g,根据牛顿惯性定律,外力等于质量乘以加速度,也就是黑色曲线纵轴对应的0.1g、0.2g…最大大约0.5g,也就是相当于大约一半的重力横着作用在了结构上面。在阪神地震作用下,小球的位移是红色曲线。横轴的时间是一一对应的,我们可以看到地震的加速度变化和小球的位移变化之间的关系。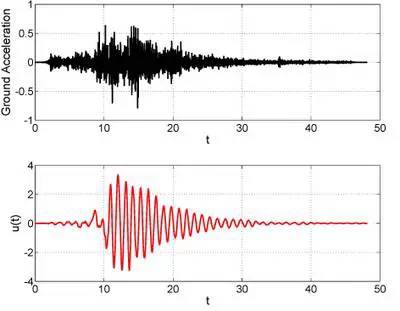
如果我们让弹簧小球经受1992年 Landers 地震,那么小球的位移则是图中的红色曲线。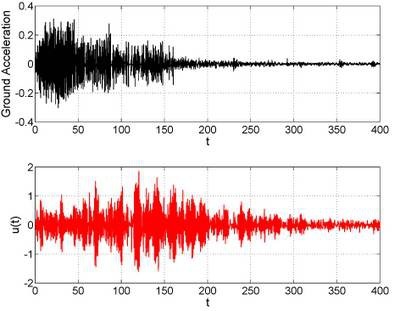
如果是2008年汶川地震呢?小球的位移则是上面的红色曲线。上面那两个地震数据都是在PEER下载的,这个是在新浪爱问下载的,所以不能确定准确与否,仅仅作为一个示例。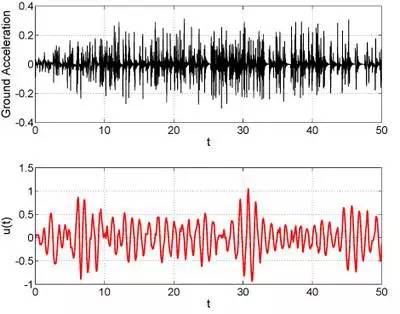
为了让汶川地震跟上面的两个地震进行比较,我们同样截取前50秒的位移。对比一下这三个地震,同样的小球,同样的结构系统,但是地震不同,尽管地震的最大加速度相近,但是造成的位移变化迥然不同。相比来说,阪神地震的位移响应非常集中,而汶川地震的持续时间非常长,来回振动的次数非常多。
考虑到这还仅仅是单个小球的「棒棒糖」模型,如果是八十层的高层建筑,最少也是八十个小球的「糖葫芦」。每个小球对应每个振型都有相应的位移响应,然后根据我们上面介绍的振型的概念,进行相应的组合叠加。如果结构体系更复杂,达不到刚性楼面的要求,那么单层还要用好多个小球来模拟。比如说,如果是跃层,那么不同高度的这两个跃层楼面就要用不同的小球来表示。这样的地震动力影响非常的复杂,必须要用大规模有限元软件才能做到足够精度的分析计算。
另外,我们考虑的都是线弹性阶段,也就是我们「棒棒糖」或者「糖葫芦」的刚度 k 不变。但事实上,随着变形的增大,结构材料可能达到屈服点,进入塑性阶段,或者结构会表现出刚度「软化」,k 随着变形的增加而减小。或者说,地震刚来的时候,结构是完好的;在地震的进行过程中,一部分结构发生了破坏,整个结构的刚度矩阵 K 跟着发生变化。也就是,不仅仅 P 和 u 是关于时间t的函数,k 也变成了关于时间 t 的函数。这使得结构分析更加的复杂。
对于实际的工程设计,我们通常会使用所谓的「反应谱」。比如央视新楼位于北京,对于北京,我们有抗震设防烈度要求,通过场地的现场地质勘探,我们能确定场地性质、剪切波速等等,继而我们能确定场地的类别、周期,继而得到该场地在某特定设防目标下的反应谱。
比如《建筑结构学报》上的《CCTV新台址主楼抗震性能研究》(清华大学 郭彦林, 霍轶力,2008)就提到了央视新楼的反应谱。反应谱是下面这样的: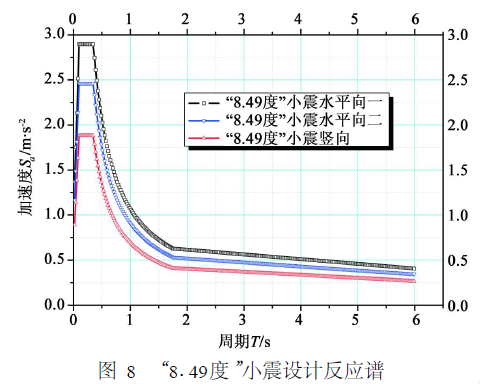
这什么意思呢?我们刚才也提到了,地震作用下同样会有「共振」的效果。反应谱体现的就是类似这样的效应。也就是说,如果我准备设计的结构的自振周期是0.1到0.5秒,那么就处在「共振」的范围内,地震加速度就会非常大。随着结构自振周期从0.5秒逐步变大,地震加速度逐步减小,也就是说,离「共振」的放大效应越来越远。
一般来说,绝大多数场地的反应谱都是这个形状的,只不过具体数值有所不同。这也就是所谓的「超高层建筑是地震中最安全的地方」。我们也说过了,结构的自振周期跟结构高度相关,一般的二三层的房子,周期0.3秒左右,刚好在「共振」的范围内。而二三十层的高层结构,周期大概1秒,对应的地震加速度已经下降了很多。至于超高层建筑,自振周期甚至能达到5秒、6秒甚至更大。在反应谱上,对应于6秒的加速度已经非常小了,带来的侧向效应可能甚至不如风荷载大。
对于央视新楼来说,钢结构,230米,一般来说,估算的自振周期大概要5秒,或者更大一些。但是,因为它独特的造型,所以它的质量分布不均匀,而且质量非常大。但是呢,它的刚度更大。这就像是和面,面加多了再加水,水多了再加面。最终的结果呢,它巨大的刚度把自振周期维持在4秒左右。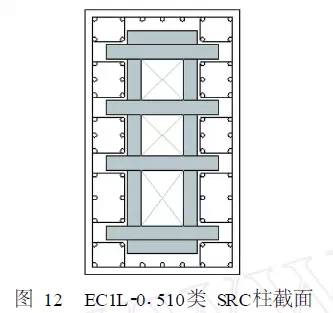
比如这是央视新楼的外圈钢框筒柱子的截面,里面是箱型钢截面,外面配上钢筋笼,最后再用混凝土浇起来。好家伙,这是多么巨大的侧向刚度。
因为央视新楼不规则的外形,我们更需要用振型分析来把握它在地震下的变形性质。
做完了模态分析,我们还得选取几条地震波,就像我们上面试的三个地震波一样,作用在分析模型上。只不过区别在于,我们上面的分析是一个小球,真正的工程设计里,可能是千千万万个小球组成的系统。
我们上面也提到了,因为分析模型的小球数量非常多,再加上刚度退化、材料屈服等非线性因素,使得实际的分析非常复杂。所以呢,对于重要的工程,我们还得用实际的缩尺模型做振动台实验,继而确定它的动力影响。
我们前面试了不同地震对于单小球「棒棒糖」体系的影响,您也能看到差别有多么的大。实际的地震千差万别,而实际的央视大楼是千千万万个小球组成的结构体系。您说,它在地震作用下会发生什么样的变形呢?因为地震的不确定性,我们回答不了这个问题;我们能做的,只是在预定的抗震设防目标下,保证结构的变形在一定的合理范围内。
相关阅读:
【行业知识】地震力到底是怎么算出来的 (1) 刚度的概念,单自由度体系的底部剪力法
【行业知识】地震力到底是怎么算出来的(2)单自由度体系的动力时程分析
【行业知识】地震力到底是怎么算出来的(3)自振周期对动力响应的影响
【行业知识】地震力到底怎么算出来的(4)等效地震加速度的反应谱
【行业知识】地震力到底怎么算出来的(5)多自由度体系的质量、刚度、自振周期
【行业知识】地震力到底是怎么算出来的(6)多自由度体系的底部剪力法
【行业知识】地震力到底是怎么算出来的(7)多自由度体系的振型
【行业知识】地震力到底是怎么算出来的(8)振型的参与系数和有效质量
【行业知识】地震力到底怎么算出来的(9)振型的动力时程响应
【行业知识】地震力到底怎么算出来的(10)振型动力时程结果的组合
【行业知识】地震力到底是怎么算出来的(11)振型组合的实用方法
【行业知识】地震力到底是怎么算出来的(12)多自由度体系的振型分解反应谱法
【行业知识】地震力到底是怎么算出来的(13)抗侧力设计实例
来源:知乎“猪小宝”、转自:,作者:猪小宝,如有侵权请联系我们。

好看