“转自:“
来源:DS结构工作室,作者:汪明
本文将与大家分享长沙“中国结桥”结构设计中的难点和解决思路,以及直接分析法应用于“中国结桥”的计算结果;

图1 桥体效果图
这是一幅“中国结”步行桥的效果图,此桥全称梅岭公园跨龙王港河步行桥,位于湖南省长沙市岳麓区梅溪湖区域,桥长约184m,宽11.5m,高约20m。目前为长沙市标志性建筑物之一,曾经也被CNN评选为“世界最性感建筑”之一。方案来自于合作伙伴北京NEXT建筑事务所,DS结构工作室承担了此桥主体转自:工作。概念源于西方“莫比乌斯环”和中国“中国结”的两种不同角度的结合,既给人创造出一个无尽的路径又象征着好远与繁荣。桥体近似由三座平行桥穿插而成,高低错落有致。无论从效果图还是实景来看,都给人以莫大的震撼。
经过多少个日日夜夜的加班加点和多少次的讨论,最终圆满交出了答卷。期间也遇到过一些问题和难点,但好歹都一一解决了。
1、通道实现及模型建立
为了便于观景与交通疏导,建筑师在平行桥桥体穿插交错位置处设置了水平通道。但由于观景需求,桥侧高度不能超过人视线,这样出桥面距离就受到限制。再者,水平转换通道的存在从结构整体性而言是对结构不利的,给结构带来突变。为了遵从建筑师的思想,我们寻找其他的突破口,看看能否以毒攻毒,利用通道处不同桥体之间的联系来实现此功能。经过不断尝试,最终选择在通道处至少保证两处桥体的完整性,采用大梁作为转换结构,同时兼做通道来实现力的有效传递和通行功能需求。
由于桥体是复杂的空间变化形体,为了充分保证模型的准确性,在初步设计阶段,借助方案提供的空间桥体模型采用偏移方式,通过先控制水平通道处尺寸后通道之间位置的顺序来实现线条模型的建立,最后由线条模型生成计算模型。

图2 穿插交错位置处水平通道
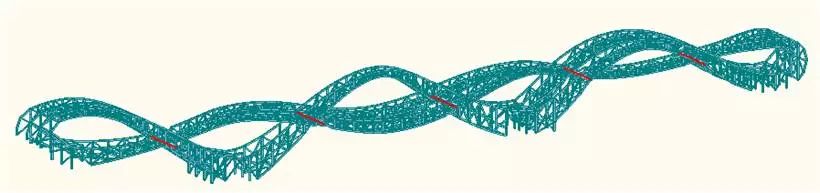
图3 穿插交错水平通道处大梁位置
2、受力体系及传力分析
面对如此形体复杂的结构,我们首先要明确其受力及传力情况,从力学概念上,对其有个清晰的认识,为此我们对此桥体进行了受力简化分析。通过对传力路径进行梳理分析,我们发现此桥虽然错综复杂,但其受力和传力路径还是相当明确的,从概念上也有了充分的心理准备。
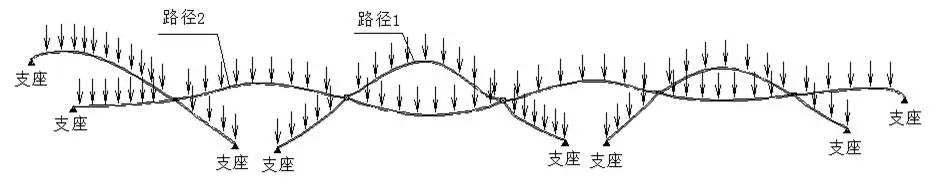
(a)计算简图
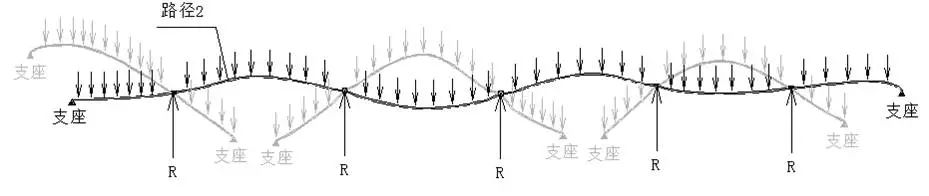
(b)路径2受力简图
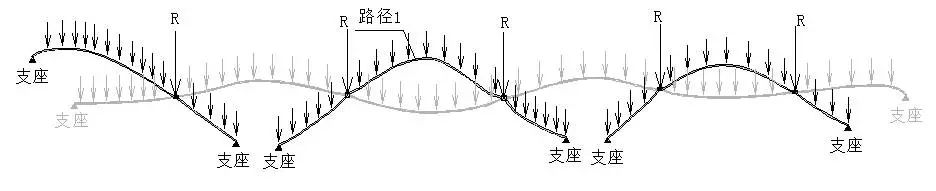
(c)路径1受力简图
图4传力路径
3、舒适度的保证
起初我们拟采用箱型梁结构方案,但经过多方试算,竖向刚度始终难以满足,为此我们不得不改变当初想法,再寻求一个刚度更大的结构方案。对于从事结构设计的人来说,截面惯性矩和截面高度关系还是十分清楚的。为了得到最大的惯性矩就必须充分利用建筑外形高度,同时考虑到结构造价这一重大经济指标,我们采用了随桥体外形变化的近似全尺寸钢桁架结构形式。即便这样,特征值分析结果也仅仅为2.79Hz(以竖向振动为主的第一竖向振型自振频率),仍不满足3.0Hz的要求。我也曾试图通过增加板件厚度即增加面积来改善频率特性,但也只是眼看用钢量大幅增加而效果不明显。为此我也苦恼过,如何才能有效地解决此问题。通过分析和不断的尝试,以及和建筑师的沟通,最终结合桥体美观要求,采用取了在穿插交错水平通道处将不同桥体之间进行一定的拉结处理,以加强竖向整体振动特性、增大竖向刚度的方式达到满足目标需求。增加少量构件、来实现大的目标,这就所谓的精准狠。
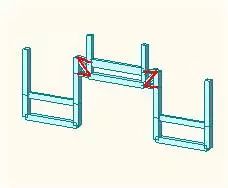
(a)做法一
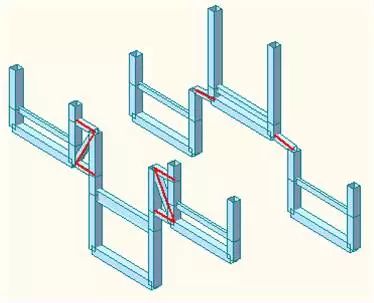
(b)做法二
图5穿插交错水平通道处拉结做法
4、计算长度确定
为满足视野通透性及通行要求,桥体桁架上弦不让设置拉结,这对于钢结构来说可不是件什么好事。首先摆在我面前的是上弦杆平面外计算长度如何确定,要知道钢结构除了强度计算外,更重要的是稳定计算。钢结构规范也没有这样的结构形式,要是上弦面外计算长度没法确认的话,设计也就无从下手。当时也听说了可以采用直接分析法,但直接分析法的前提是缺陷的考虑。对于一个如此多单元的模型,如何考虑初始缺陷等,对于当时的我来说确实是个难题。如果拿到现在来说,直接分析法也就不是个问题,可以通过NIDA软件开发的自身缺陷单元来实现,但对于当时孤陋寡闻的我来说,确实是个难以实现的方式。好在,后来经过大量文献资料查阅,在老前辈陈绍蕃《钢结构稳定设计指南》一书中,找到了参考方式,依靠腹杆的抗弯刚度来保证上弦杆的稳定性。
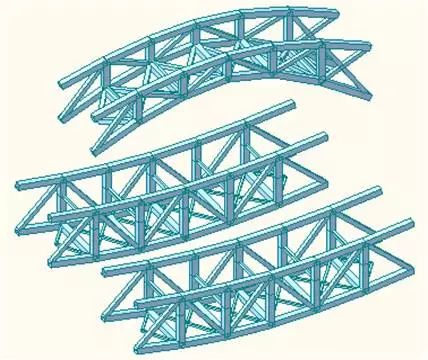
图6 桥体钢桁架结构
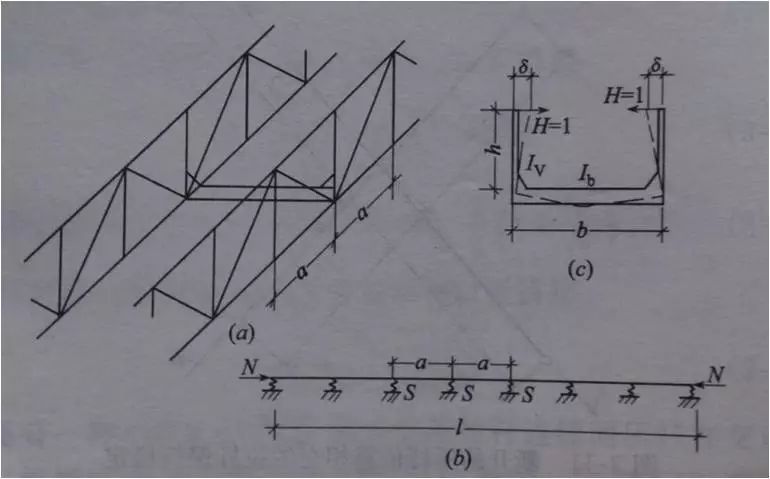
图7 不设支撑系统的桁架受压弦杆的稳定计算


这座桥的结构设计涉及诸多关键技术,其中最不起眼的桥梁栏杆便是其中一项。其核心设计难点便是栏杆的面外稳定问题。
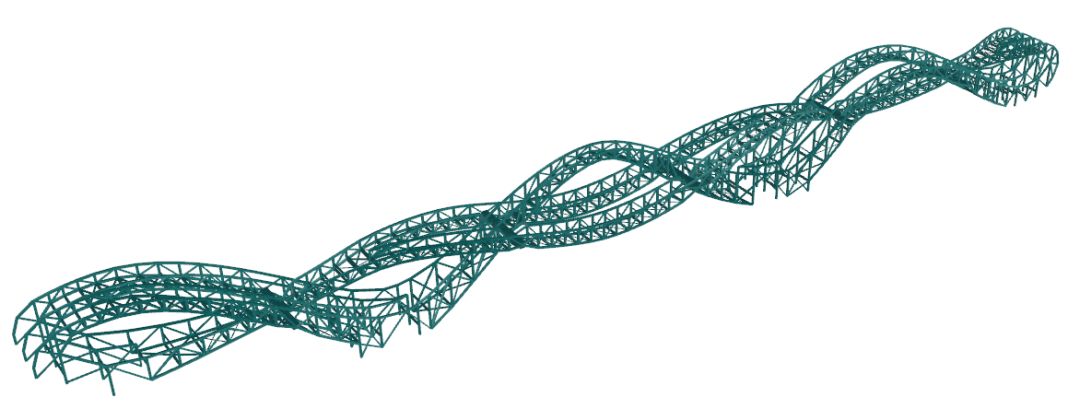
与普通桥梁栏杆不同,本桥的栏杆是结构主受力杆件,其设计合理性事关该桥梁的整体安全性。如上图所示,本桥梁的结构是由若干飘带状桁架组成,栏杆便是桁架的上弦杆。

桁架上弦杆受压是所有结构工程师所熟知的常识,受压杆的面外稳定也是工程师们所担心的问题。在本桥中,作为受压杆的栏杆恰恰没有任何面外支撑体系。因此,在结构设计中,栏杆的面外稳定是设计难点之一。
陈绍蕃教授的著作《钢结构稳定设计指南》中提到一种此类问题的近似计算方法,该方法也在桥梁领域普遍使用。
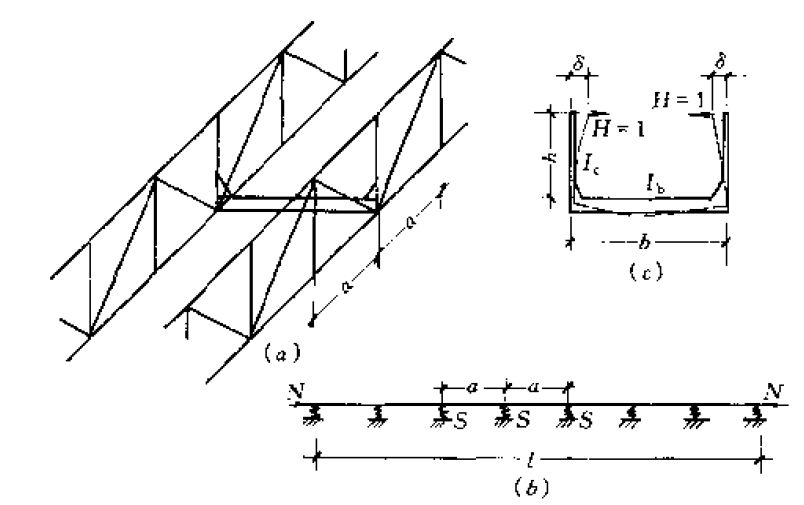
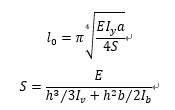
该简化方法的核心思想是将由桥梁横梁和栏杆竖杆组成的C型截面的面内刚度考虑为栏杆的面外约束刚度,而栏杆的计算长度取决于横梁和竖杆的刚度。
然而,正如在陈老先生在其著作中提到的,该方法过于保守,其原因如下:
(1)弦杆内力是变化的,N由中部向两端减小。如果截面惯性矩保持常量或改变不大,则N的临界值将提高。
(2)当弦杆在非弹性范围屈曲时,它的刚度比弹性值下降,此时槽形框架因受力不大而处于弹性范围,所提供的约束作用相对提高,也使NCR提高
(上述文字引自《钢结构稳定设计指南》(作者:陈绍蕃))
下图是基于上述近似方法进行一阶线性计算和设计后的杆件应力比。从中我们可以看到栏杆杆件的应力比已经超过0.8,拱桁架相交处的部分杆件接近1.0。因此,采用一阶设计方法基本没有进一步优化的空间。
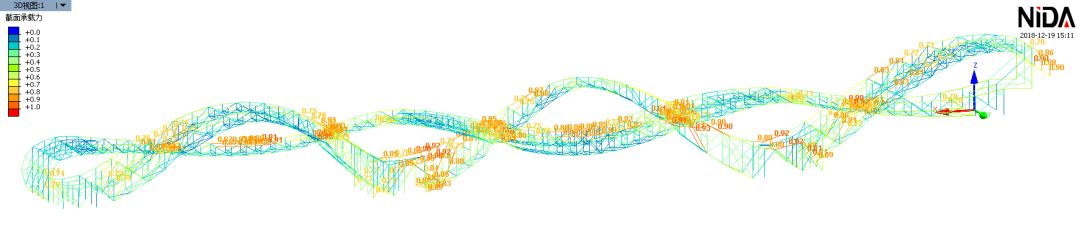
作为转自:领域的一项黑科技——直接分析法,正在被越来越多的工程师认知和接受。下面我们来看看当“性感“遇上“黑科技”后将会发生什么。
在以往的一个多世纪内,结构工程师迫于计算工具局限性只能通过“计算长度系数”考虑边界刚度对杆件稳定性的影响,并通过“稳定系数”考虑受压杆件的强度折减。对于简单的结构体系,这套传统稳定近似计算方法是完全可以胜任的。然后,随着建筑形态的复杂化和多样化,准确估算计算长度系数已越来越成为一种奢望。另一方面,各种各种的几何非线性问题出现在工程领域,如张弦结构、索膜等柔性结构等,一阶计算已不再适用于高级设计的需求。
直接分析法的横空出世,使被逼入绝境的结构设计领域看到了曙光。早在十多年前,直接分析法已出现在美国规范、欧洲规范、香港规范等,并且以主要推荐设计方法出现。


随着我国新版《转自:标准》(GB50017-2017)的发布,直接分析法也开始被国内广大结构工程师们青睐。
直接分析法的本质理念是:让结构计算回归真实的力学状态。换言之,使用直接分析法的最终目的是在计算过程中避免或尽量减少采用假定和假设。在钢结构稳定计算方面,采用直接分析法将摒弃计算长度系数和稳定系数的概念,而是直接通过考虑构件和结构缺陷,并计算在结构受力过程中缺陷对结构刚度的影响,实现对钢结构失稳问题的真实分析。
仅考虑第一个塑性铰的直接分析法的基本设计步骤可用下述流程图表述:
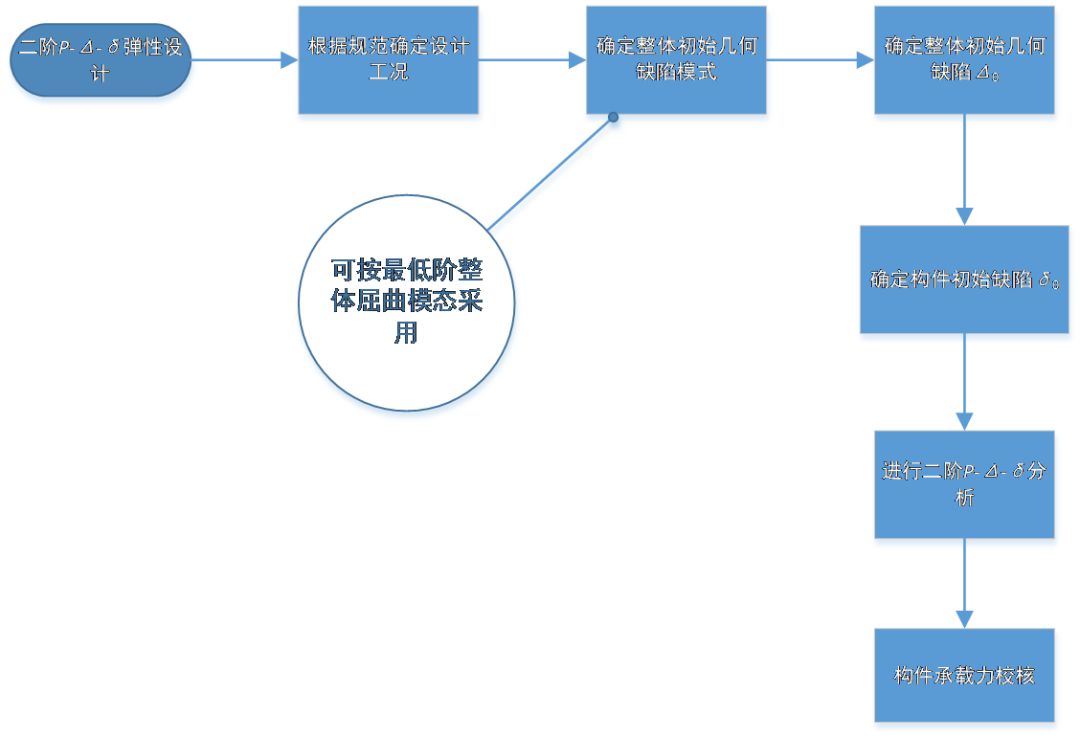
将直接分析法应用于本工程中,可得到所有杆件的应力比,如下图:
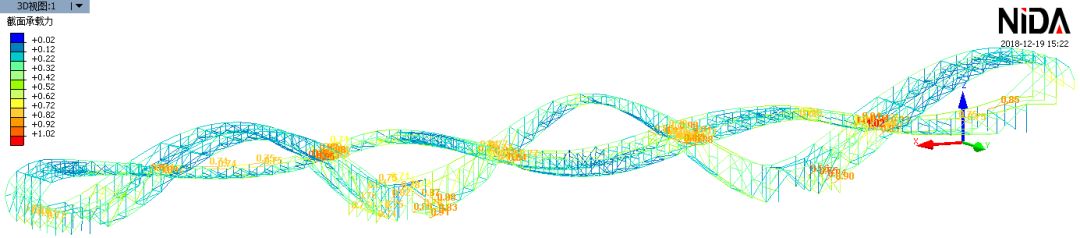
从这个图所表示的计算结果看,大部分栏杆和竖杆的承载力有富裕,意味着原来估算的计算长度过大(验证了陈老对上述简化方法的评论)。
基于直接分析法的计算结果,对该结构进行优化。主要优化思路如下:
1、加强容易发生失稳区域的杆件;
2、减小不易发生失稳区域的杆件优化后,结构的计算结果如下图:
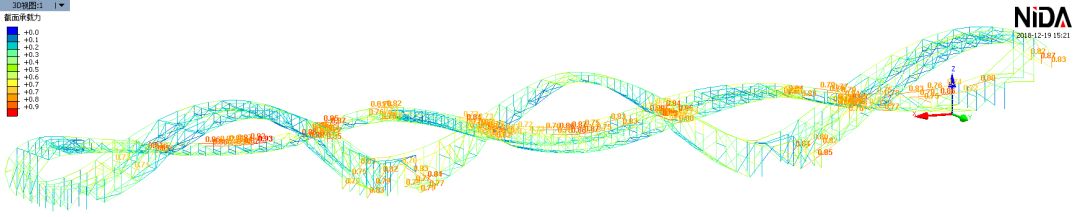
对比优化前后的杆件应力状态,应力集中处的最大应力比有所下降,栏杆和竖杆截面减小显著,其应力比有明显上升,但基本在0.9以下,仍处于安全范围。总体而言,优化后杆件的应力分布更加均匀、合理。
从经济性上看,结构用钢量优化了18%。
另外,由于栏杆和竖杆截面的减小,使桥梁更加美观。如下图:
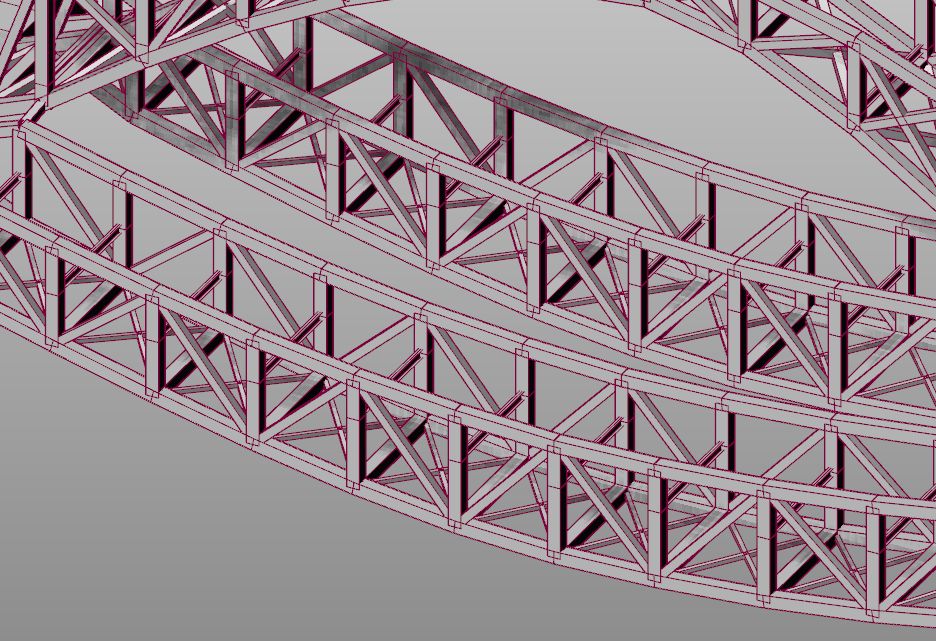 优化前▲
优化前▲ 
优化后▲
可见直接分析法的应用可使造型性感的“中国结“桥更加“苗条”,大幅提高该建筑的整体美观。
虽然直接分析法的结果也是通过应力或应力比来体现,但其意义与一阶计算结果的应力比有所不同。由于其非线性的本质特征,直接分析法应力比(应力比与1.0的差距)不能说明结构的安全冗余度,但我们可以通过弹塑性极限承载力分析进一步了解结构在超过设计荷载时的状态。
下图所示动画为该桥在以(1.35恒荷载+0.98活荷载)为基本荷载条件下进行极限承载力分析的塑性铰发展过程:

从整个过程看,桥梁栏杆未发生几何失稳,而是先发生材料屈服。下图所示是当荷载系数为2.7时对应的塑性铰分布情况。

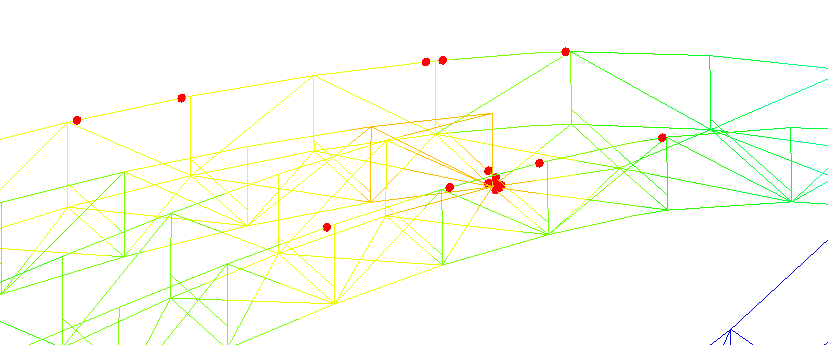
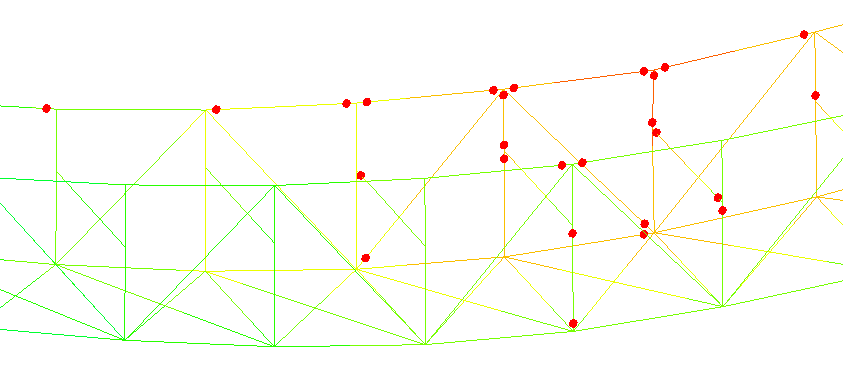
结合直接分析法和弹塑性极限承载力分析的结果,我们有理由相信“瘦身”后的“中国结”是足够安全的。
优秀的建筑作品被誉为“凝固的交响乐“,为了能给这个世界留下更多优美的“交响乐”,我们结构工程师需要利用我们的知识将更多出色的建筑作品成为现实,而直接分析法必然成为我们手中又一把利器。

新钢标的相关阅读:
《转自:标准》解说专题(0)—钢结构的材料选择
《转自:标准》解说专题(1)—截面等级
《转自:标准》解说专题(2)—新术语解释
《转自:标准》解说专题(3)—新钢标与现行规范的逻辑关系及应用
《转自:标准》解说专题(6)—节点域设计
《转自:标准》解说专题(7)—疲劳计算
【转自:】如何按新钢标控制宽厚比?
【钢构知识】钢结构计算参数和构造要求 (2017版新钢标)
【转自:】新钢标的钢结构性能设计流程及案例分享
【钢构知识】GB 50017-2017《转自:标准》简述
《转自:标准》勘误表
来源:DS结构工作室,作者:汪明,如有侵权请联系我们。

咨询和建议,请加下方小编个人微信
好看