 "转自:"
"转自:"
上一篇文章讨论了应变能作为结构效率评判标准的理论依据,因此,我们在结构优化时,就可以将应变能作为优化目标。但是,结构优化能否得到一个绝对最优的解?小i觉得这是要打上一个问号的。
结构优化解的多样性
仍然使用经典二力杆案例进行分析。
示例:有两根相互铰接的二力杆,两端是铰接支座,支座间距为2L,假设L为常数,θ为变量,中间受到一个竖直向下的集中力F作用,如图1所示。
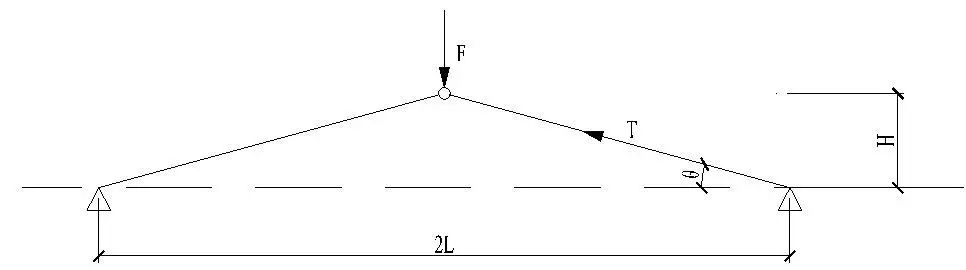
图1 二力杆示例计算简图
单根杆件轴力:
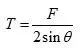
单根杆件变形:
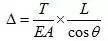
整个结构应变能:
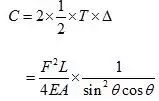
1)截面为常量,应力为变量
这个假定在上一篇示例中没有明确,在此强调一下。如给您带来困惑,表示歉意。则求解应变能的极值就是求解以下函数的极值:
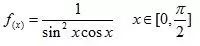
以上函数的极值点为x=0.955,对应极值为f(x)=2.5981。
所以假设杆件截面不变,当θ=54.76°时,应变能最低,结构刚度最大。
2)应力为常量,截面为变量
假设应力为常量,那么截面积A就是一个随θ变化的变量。
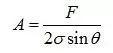
应变能的表达式就要改写为如下:
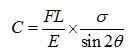
由上式可知,应变能在θ=45°时最小。即控制杆件应力水平相同,当θ=45°时,应变能最低,结构材料用量最小。
3)H为常量,L为变量
上一篇示例1)中已有推导,在此仅给出结论。应变能的表达式如下:
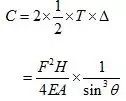
可见,应变能在θ=90°时最小。所以,如果截面恒定,θ=90°时结构刚度最大;如果应力比恒定,θ=90°时材料用量最小。
以上都是以应变能为优化目标,但是当约束条件不同时,得到的结果不同。若进一步改变优化目标,看下优化的结果是什么?
4)截面不变,考虑压杆稳定,以最大承载力为优化目标
首先欧拉公式为:
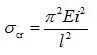
将杆件长度与L和θ的关系代入上式,可得:
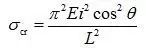
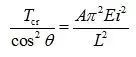
进而可以得到外力F与θ的关系:
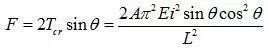
由上式可知,θ=35.26°时,相同的杆件截面可以承受最大的外力F。
可见,不同的约束条件、不同的优化目标,得到的结构形态都是不同的。小i在实际的优化实践中觉得,假定截面为常量进行优化比较可行。
比如在进行形态优化时,将截面设定为常量将会减少非常多的优化变量,这样仅需将优化变量设定为节点坐标,计算工作量大大下降。而这样做可以得到一个相对较优的解。下图即为采用该种方法进行形态优化的一个示例。

结构效率系数—结构效率的另一个指标
之前探讨了应变能作为作为结构效率的评价指标,但是小i还想探讨结构效率的另一个指标,我称之为“结构效率系数”。这个指标的物理意义存疑,但小i仍觉值得讨论。
如果我们将结构的传力类比于“工作总量”和“工作时间”,我们是不是能够将结构效率类比于“工作效率”呢?
“工作总量”——外力势能(W)
我们将外力F与外力到传力目的地的距离s的乘积定义为外力势能W:
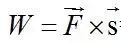
规定:支座位置为外力的势能零点。
“结构的工作时间”——结构应变能(C)
在应力比水平相同的情况下,我们用应变能的大小反映结构传递外力所要耗费的材料。
“工作效率”——结构效率系数(μ)
结构效率系数=外力势能/结构应变能
μ=W/C
基于此,再看以下示例:有两根相互铰接的二力杆,两端是铰接支座,支座间距为2L,假设L为常数,θ为变量,中间受到一个竖直向下的集中力F作用,如图2所示。
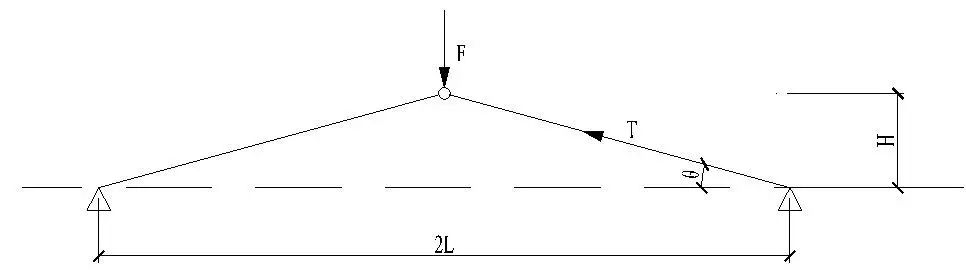
图2 二力杆示例计算简图
外力势能:
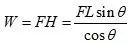
结构应变能:
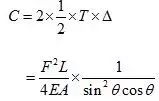
结构效率系数:
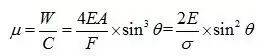
可见,不管是应力比为常量还是截面面积为常量,都是θ=90°时结构效率系数最高。
但是,θ=90°,外力势能趋于无穷大,材料用量也趋于无穷大。
假设H为常量,L为变量
外力势能:
W=FH(定值)
结构应变能:
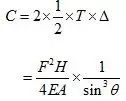
结构效率系数:
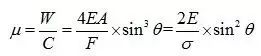
由上式可得,θ=90°时,结构效率系数最大,同时,结构应变能最小。
可见,如果以“结构效率系数”为指标,则用应变能优化得到的不同解统一为一个解。关于这个指标中的“外力势能”,小i解释不清。对于一根悬臂梁,在自由端作用一个集中力,外力势能应该是力与力臂的乘积。但通常我们认为,力与力臂的乘积是力矩。虽然小i知道,力矩是矢量、势能是标量。但巧的是,他们的单位都是kN.m。所以,小i觉得这两个物理量之间是不是统一的?但目前为止,还没想通。如果您有想法,欢迎留言。
弗雷·奥托研究轻型结构时,也采用了类似的指标来研究结构的受力效率。他认为“力臂、力传递距离、输送能力等专业名词,他们有着相同的基本意义”。有兴趣的朋友可以查阅《轻型建筑与自然设计—弗雷·奥托作品全集》。
小结
▲力沿刚度最大的路径传递,但并不代表刚度最大的路径结构效率最高。最短的路径才是力流传递是最有效率的,材料是最省的或刚度是最大的。
▲应变能可以一定程度代表结构的材料用量和结构刚度,因此结构优化中可以将它作为优化指标,且建议实际优化中假定截面是不变的。
▲不同的约束条件、不同的优化目标所导致的优化结果可能不一样。优化得到的解往往是一个相对优的解,而不是绝对最优解。
▲介绍了一个概念“结构效率系数”,这是一个有争议的概念,且在结构设计中暂时看不到应用。
小i设计资历尚浅,文中很多说法不严谨,特别是对于某个概念(外力势能),暂时没有办法明确其物理意义。但是,小i觉得文中看待结构效率的一些角度,可能是有启发的,希望您读了以后有所收获。欢迎留言讨论,欢迎拍砖。
转载本文请注明出处 iStructure微信公众号,作者:海盗猪。已获得原作者授权。
开设iStructure公众号的初衷是分享结构工程领域的见闻、优秀的设计和自己一些不太成熟的思考,向更多人呈现结构设计有趣的一面。