 "转自:"
"转自:"
上一篇我们讨论了如何从各振型的最大值估算组合之后的最大值。掌握了这个估算的方法,我们就可以把我们早已得出的反应谱利用起来,代替繁复的时程分析。这也就是我们常说的振型分解反应谱法。
还是我们的三层小房子,我们已经得到了特征矩阵和振型参与系数。
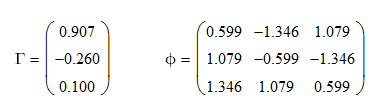
在 part.11 里我们从参与系数和特征矩阵出发,得到了振型的组合系数。
同时,我们还知道这个三层房子的三个自振周期:
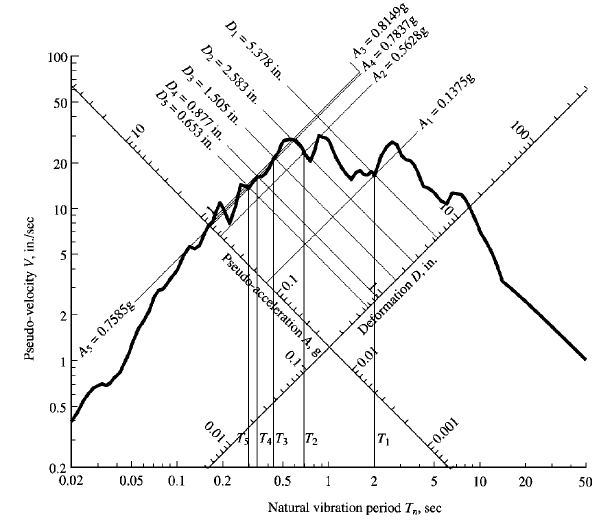
在 part.6 里,我们利用反应谱求出了对应于第一周期的地震影响系数。也就是反应谱中横坐标对应0.547秒,纵坐标为 0.134。
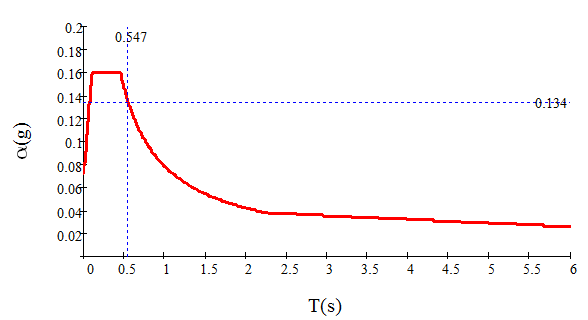
同样的道理,我们可以得到对应第二周期和第三周期的地震影响系数。
也就是说,对应三个自振周期,我们得到了三个地震影响系数。
下一步,我们就可以得出各个振型的地震作用力。
对于第一振型,我们已经知道了下面这些东西:
第一振型的地震作用力,就是
看起来挺复杂,其实就是把地震影响系数、组合系数、各楼层的重力相乘,也就是
第一振型的地震作用力,就是一层 215 千牛、二层 387 千牛、三层 482 千牛。
同样的道理,我们可以得到第二振型、第三振型的楼层地震力。
到这一步,我们已经得到了三个振型的楼层地震力。
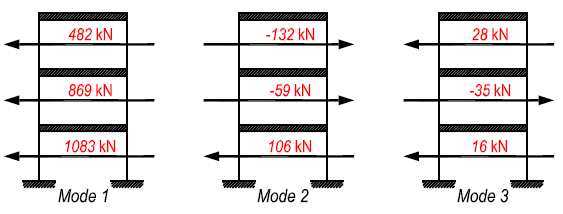
我们已经说过好几次,如何从楼层地震作用力得到楼层地震剪力。各个振型的楼层地震剪力是这样的:
接下来,我们上一篇讲的 ABS、SRSS、CQC 三种方法就派上用场了。
对于一层的地震剪力,第一振型 1083、第二振型 106、第三振型 16,ABS 的组合结果是 1205,SRSS 的结果是 1088,CQC 的结果是1090。
同样的道理,我们也能得到二层和三层的地震剪力。
注意到,在 part.6 里我们用简化的地震剪力法也求得了各楼层的地震剪力。我们把这些结果列在同一个表格里,做一个比较:
ELFM 其实也就是底部剪力法,Modal Analysis 是振型分解,振型组合的方法有三种,分别是 ABS、SRSS、CQC。注意到 SRSS 和 CQC 结果比较接近,而且它们两者的结果要比底部剪力法和 ABS 的结果小一些。
在我们这个小例子里,楼房只有三层,并且只考虑一个方向的地震。我们在之前说振型的意思的时候也说了,三层楼房实际的振型至少有9个,因为每一层都可以南北方向、东西方向、上下方向运动。对于30层、50层的高层建筑,那振型的数量就更多了。但是,我们也注意到,越是排在后面的振型,对于最终结果的影响越小,有时候甚至小到可以忽略不计。那么我们如何考虑这些振型呢?什么时候可以省略?什么时候不应该省略呢?
我们在 part.9 里提到了有效参与质量的概念,也就是各个振型的 Mstar。
第一振型的有效质量占了 91.4%,第二振型占 7.5%,第三振型 1.1%,三者加起来等于 100%。
如果都采用 SRSS 组合,我们可以看一下如果我们只考虑第一振型、第一加第二振型、第一加第二加第三振型的结果。
以底层剪力来看,只考虑第一振型,地震剪力为 1083;考虑进第二振型,地震剪力为 1088;再考虑上第三振型,还是 1088。也就是说,第三振型几乎没有任何作用。
通常来说,判断的标准是有效质量总和超过90%。在我们的例子里,第一振型 91.3%,已经超过了 90%,所以,简化计算的话,我们只考虑第一振型就足够了。
比较一下只考虑第一振型的数值,和三个振型都考虑之后 SRSS 的结果,第一层、第二层的地震剪力误差不超过 0.5%,第三层剪力误差大约 4%。
如果第一振型 60%,第二振型 32%,第三振型 8%,为了达到有效质量总和超过 90%,我们就必须得考虑第一振型加第二振型。这两者有效系数之和为 92%,超过了 90%。这时候,第三振型就可以忽略不计。
对于更多振型的情况也都是如此,从第一振型开始累加,直到超过 90% 为止,后面的振型就可以忽略不计,因为后面这些振型的作用实在太小,几乎不会对结果造成什么影响。
这就是振型分解反应谱法的全过程。既利用振型分解更好的体现了结构的动力特性,同时又利用反应谱方便快捷的得到可靠的地震作用效应,相对来说,是一个合理简洁的工程实用方法。
地震力到底是怎么算出来的,到这里说的已经差不多了。下一篇,我就举一个小例子,从工程实例的角度出发,看一下抗震设计的大致步骤。
来源:知乎。作者:猪小宝。如有侵权请联系删除。



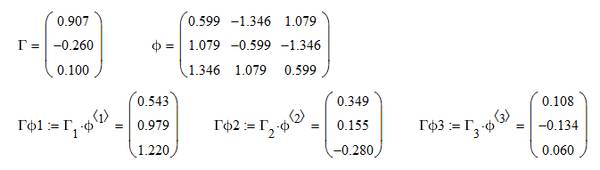 同时,我们还知道这个三层房子的三个自振周期:
同时,我们还知道这个三层房子的三个自振周期: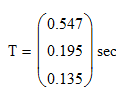 在 part.6 里,我们利用反应谱求出了对应于第一周期的地震影响系数。也就是反应谱中横坐标对应0.547秒,纵坐标为 0.134。
在 part.6 里,我们利用反应谱求出了对应于第一周期的地震影响系数。也就是反应谱中横坐标对应0.547秒,纵坐标为 0.134。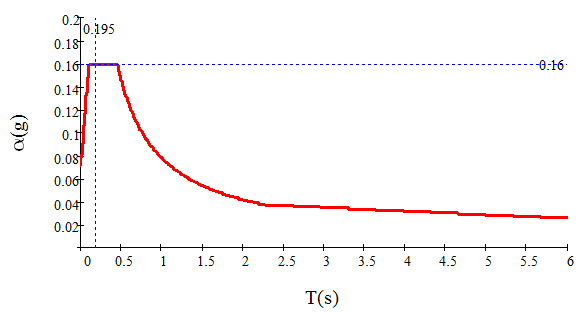
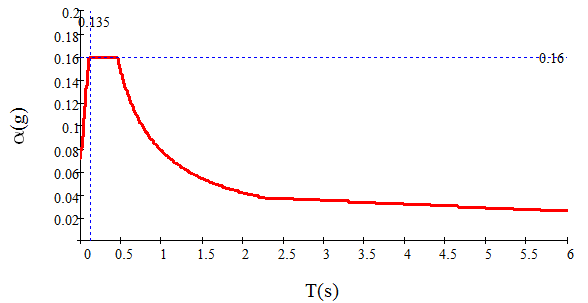 也就是说,对应三个自振周期,我们得到了三个地震影响系数。
也就是说,对应三个自振周期,我们得到了三个地震影响系数。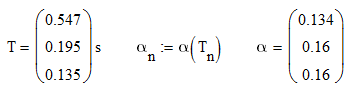 下一步,我们就可以得出各个振型的地震作用力。
下一步,我们就可以得出各个振型的地震作用力。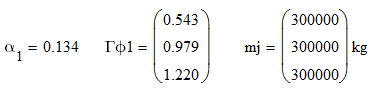 第一振型的地震作用力,就是
第一振型的地震作用力,就是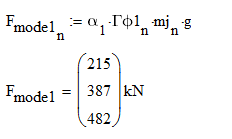 看起来挺复杂,其实就是把地震影响系数、组合系数、各楼层的重力相乘,也就是
看起来挺复杂,其实就是把地震影响系数、组合系数、各楼层的重力相乘,也就是 第一振型的地震作用力,就是一层 215 千牛、二层 387 千牛、三层 482 千牛。
第一振型的地震作用力,就是一层 215 千牛、二层 387 千牛、三层 482 千牛。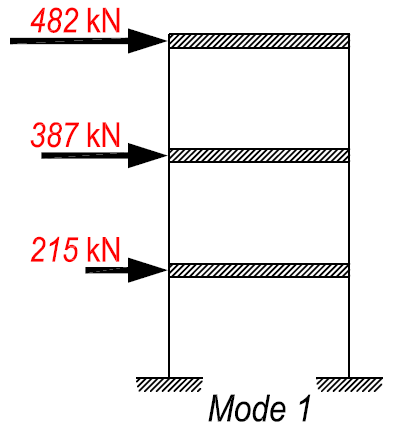 同样的道理,我们可以得到第二振型、第三振型的楼层地震力。
同样的道理,我们可以得到第二振型、第三振型的楼层地震力。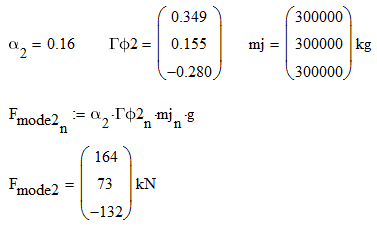
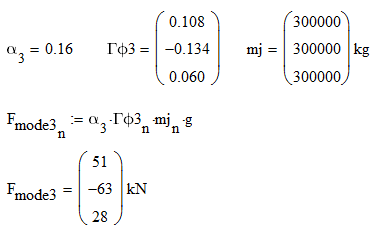 到这一步,我们已经得到了三个振型的楼层地震力。
到这一步,我们已经得到了三个振型的楼层地震力。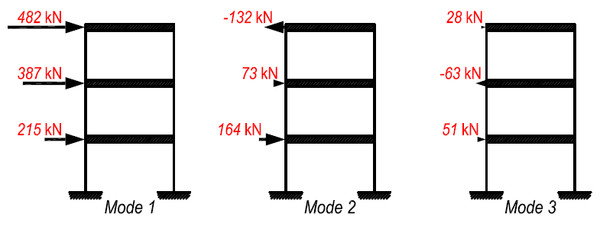 我们已经说过好几次,如何从楼层地震作用力得到楼层地震剪力。各个振型的楼层地震剪力是这样的:
我们已经说过好几次,如何从楼层地震作用力得到楼层地震剪力。各个振型的楼层地震剪力是这样的: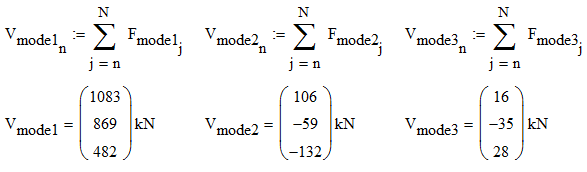
 接下来,我们上一篇讲的 ABS、SRSS、CQC 三种方法就派上用场了。
接下来,我们上一篇讲的 ABS、SRSS、CQC 三种方法就派上用场了。 对于一层的地震剪力,第一振型 1083、第二振型 106、第三振型 16,ABS 的组合结果是 1205,SRSS 的结果是 1088,CQC 的结果是1090。
对于一层的地震剪力,第一振型 1083、第二振型 106、第三振型 16,ABS 的组合结果是 1205,SRSS 的结果是 1088,CQC 的结果是1090。 注意到,在 part.6 里我们用简化的地震剪力法也求得了各楼层的地震剪力。我们把这些结果列在同一个表格里,做一个比较:
注意到,在 part.6 里我们用简化的地震剪力法也求得了各楼层的地震剪力。我们把这些结果列在同一个表格里,做一个比较: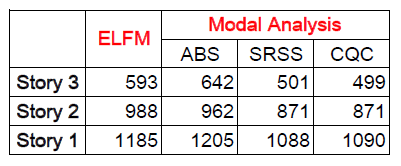 ELFM 其实也就是底部剪力法,Modal Analysis 是振型分解,振型组合的方法有三种,分别是 ABS、SRSS、CQC。注意到 SRSS 和 CQC 结果比较接近,而且它们两者的结果要比底部剪力法和 ABS 的结果小一些。
ELFM 其实也就是底部剪力法,Modal Analysis 是振型分解,振型组合的方法有三种,分别是 ABS、SRSS、CQC。注意到 SRSS 和 CQC 结果比较接近,而且它们两者的结果要比底部剪力法和 ABS 的结果小一些。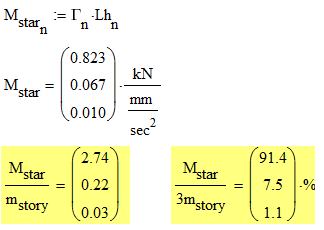 第一振型的有效质量占了 91.4%,第二振型占 7.5%,第三振型 1.1%,三者加起来等于 100%。
第一振型的有效质量占了 91.4%,第二振型占 7.5%,第三振型 1.1%,三者加起来等于 100%。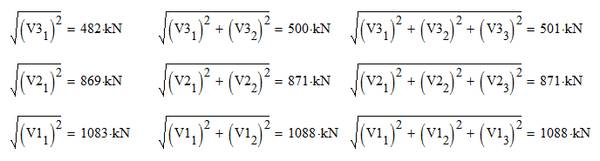 以底层剪力来看,只考虑第一振型,地震剪力为 1083;考虑进第二振型,地震剪力为 1088;再考虑上第三振型,还是 1088。也就是说,第三振型几乎没有任何作用。
以底层剪力来看,只考虑第一振型,地震剪力为 1083;考虑进第二振型,地震剪力为 1088;再考虑上第三振型,还是 1088。也就是说,第三振型几乎没有任何作用。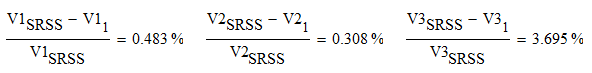 比较一下只考虑第一振型的数值,和三个振型都考虑之后 SRSS 的结果,第一层、第二层的地震剪力误差不超过 0.5%,第三层剪力误差大约 4%。
比较一下只考虑第一振型的数值,和三个振型都考虑之后 SRSS 的结果,第一层、第二层的地震剪力误差不超过 0.5%,第三层剪力误差大约 4%。